What faces does a parallelepiped consist of? Rectangular parallelepiped – Knowledge Hypermarket

During the classes
Before the start of the lesson, the teacher checks the students’ readiness for the lesson: readiness
boards, order on desks, presence of notebooks. Notebooks are collected before class.
IMotivational - orientation stage
Home building inspection. Update.10 min
Ready for the lesson. Checking the availability of supplies needed for the lesson.
- What figure is shown in the picture?

Rectangle ABCD.
- Name the elements of rectangle ABCD.
- Vertices A, B, C, D; sides: AB, BC, CD, AD
- Are the following statements true:
1. A rectangle has 4 vertices and 4 sides.
2. Each side of the rectangle is a straight line, the apex is a point.
3. A rectangle has all sides equal.
What is the name of a rectangle whose sides are all equal?
4. In a rectangle, opposite sides are equal. Give an example of opposing sides.
- 1. That's right.
2. Incorrect. Each side of the rectangle is a line segment, and the vertex is a point.
3. Incorrect. A special case.
Square.
4. True. Opposite sides: AB and DC, AD and BC.
- Make up a problem based on the drawing.
How to calculate the area of a rectangle?
- To find the area of a rectangle, you need to multiply the length by the width.
- Write down the formula for calculating the area of a rectangle.
- S= ab
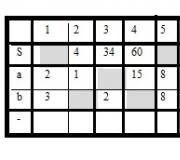
- Exercise. Orally find the unknown component in the table. First line area
rectangle, the second and third row are the sides of the rectangle. IN
According to the key, for each answer received, substitute the correct letter.

The calculation is performed frontally in the classroom. One by one, students make calculations in the table and enter the correct answer.
- What word did we receive?
- Parallelepiped.
- What is it?
- This is a volumetric geometric body.
- These bodies are divided into two groups: the upper 4 bodies and the lower ones. On what basis are they divided into two types? What do the bodies in each group have in common?

The upper bodies are polygonal, and the lower bodies are round. In the upper group, each body consists of polygons, and in the lower group, one of the elements is a circle.
- We are surrounded by many objects in the world. They differ in shape, size, materials from which they are made, color... People are interested in the different qualities of these objects. Mathematicians are interested in their shape and size. Among the many geometric bodies, there are two large groups: polyhedra and round bodies.
The word we received is a parallelepiped, which means a three-dimensional body, which is one of the types of polyhedra.

- Which of these polyhedra are parallelepipeds?
- Bodies A, B
- What distinguishes them from the remaining polyhedra?
- The faces are rectangles.
- Give examples of objects from the surrounding world that have the shape of a rectangular parallelepiped?
- Textbook, house frame, classroom, box.
- The study of spatial bodies occurs in 10th grade, we will study the section of geometry - stereometry, but in 5th grade
we can already give some initial information about volumetric figures,
get acquainted with its elements and some properties.
What is the purpose of today's lesson?
- Get acquainted with the elements that make up a rectangular parallelepiped.
Operational - cognitive stage. 20 minutes
1. Write down the topic of the lesson in your notebooks.
Number, class work and lesson topic.
2. Before us are several models of a rectangular parallelepiped: a wooden model, as well as a frame model. On these models, the elements of a rectangular parallelepiped are clearly visible.
Show faces, edges, vertices of the parallelepiped on the model.
There are a certain number of these components. Let's count how many there are. Let's fill out the table.
The teacher calls students to the board to count the number of vertices, edges and faces.
The table is filled in parallel
(the first two columns are filled in):

- So, as we know any point in space and on the plane, we can denote it with a Latin letter of the alphabet.
Here is an image of a rectangular parallelepiped. Each vertex was designated by a Latin letter. Listing
Latin letters, we denote this parallelepiped. Who can tell me how this parallelepiped is designated?
- ABCDKLMN
- Exercise.
1. the first row writes out the designation of the vertices;
2. second designation of ribs;
3. third row - designation of edges.
To present the results, students come to the board in pairs. One reads out the elements, the second shows them on the drawing.
If addition is needed, the teacher turns to other groups.
- Find equal edges for the parallelepiped.
- AB= DC = MN = KL
AK = BL = CM =DN
AD = BC = LM =KN
Students write in their notebooks.
- Each group of equal edges has names.
AB = DC= MN= KL - width
AK= BL= CM= DN - length
AD= BC= LM= KN - height
- Is it possible for all three dimensions to be equal?
- Yes.
- What figure do we get?
- Cube.
- From early childhood we have been familiar with such a figure as a cube.
What are the differences between a cube and the general form of a rectangular parallelepiped?
- The cube has all equal edges. All faces are squares.
- Which sides will be equal for the parallelepiped ABCDEFGH.
At the same time there is a slide show.

- ABCD = KLMN
ADNK=BCML
ABFE=DCGH
- How these edges are mutually located relative to each other.
- They lie opposite each other.
- Such faces are called opposite to each other.
What conclusion can be drawn from the above?
- Opposite faces of a rectangular parallelepiped are equal.
Both on the slide and on the model, equal edges are highlighted in the same color.
- Opening textbook on page 121,№ 792.
What is the surface area of a rectangular parallelepiped?
- The sum of the areas of its faces.
- How many faces does a parallelepiped have?
- 6
- What geometric shapes are these faces?
- Rectangles.
- How to calculate the area of each face?
- Find the product of measurements for each face of the parallelepiped.
- What properties do the faces of a parallelepiped have?
- Opposite sides are equal.
- Therefore, we will find the area only on three faces.
- What are the measurements of the first face?

- 5 cm and 6 cm 5∙6=30 cm2
- What are the measurements of the second face?
Calculate the area of this face.
- 5 cm and 3 cm 5∙3=15 cm2
- What are the dimensions of the third face?
Calculate the area of this face.
- 3cm and 6cm 6∙3=18 cm2

- 2∙30+2∙15+2∙18=126 cm2
- How to express the surface area of a rectangular parallelepiped?
No. 796 (b) - Write a formula to calculate the surface area of a rectangular parallelepiped.
- Measurements of the first face a and b
S= a∙b
Measurements of the second face b and c
S=b∙c
Third face measurements a and c
S=a∙c
S=2∙ab+2∙bc+2∙ac
- So, we have derived a formula by which it is easy to find the surface area of a rectangular parallelepiped, knowing its measurements.
Task:
The boy wants to pack a gift prepared for his mother for the New Year in a box shaped like a rectangular parallelepiped, the dimensions of which are 20 cm.*30cm×40 cm He decided to cover this box on all sides with colored paper, 1 dm2 of which costs 8 rubles. The boy expects to spend 450 rubles to buy the required amount of paper. Will he have enough money for this?
- First, let's find the surface area of the parallelepiped.
S=2∙ab+2∙bc+2∙ac
1) 2∙20∙30+2∙30∙40+2∙20∙40=1200+2400+1600=5200 cm 2 is the surface area of the parallelepiped.
2) 5200 cm2 =52 dm2
3) 52∙8=416 (RUB) - required for purchase.
Answer: The boy can safely go for colored paper.
III Reflective-evaluative stage
First we will write down our homework and then we will summarize our lesson.
§4, paragraph 20, page 121 no.811,812, 814, 817.
Clear recommendations for performing each number.
- What was the purpose of our lesson?
- Study the components and properties of a rectangular parallelepiped.
- Have we achieved this goal?
- Yes, we have achieved it.
- Name objects from the surrounding world that have the shape of a rectangular parallelepiped.
- Houses, class, brick, etc.
- What elements have we identified in a rectangular parallelepiped?
- Vertices, edges and faces.
- How many vertices, edges and faces does a rectangular parallelepiped have?
- Peaks - 8; ribs - 12; faces - 6.
- Name the dimensions of a parallelepiped.
- Length Width Height.
- Name the properties of the faces of a parallelepiped.
- Opposite faces of a parallelepiped are equal.
- How to find the lateral surface area of a rectangular parallelepiped.
- We need to add up the areas of the faces of the parallelepiped.
- Why do we need to find the area of the lateral surface of a parallelepiped?
- For practical purposes. For example, to cover a box with paper, paint a room, or wallpaper a room.
- So, the lesson is over, but put a grade in your notebook for your work in class, and add + to this grade
- if the lesson was interesting for you;
- if the lesson was boring.
Thank you for your attention!

or (equivalently) a polyhedron with six faces that are parallelograms. Hexagon.

The parallelograms that make up a parallelepiped are edges of this parallelepiped, the sides of these parallelograms are edges of a parallelepiped, and the vertices of parallelograms are peaks parallelepiped. In a parallelepiped, each face is parallelogram.

As a rule, any 2 opposite faces are identified and called bases of the parallelepiped, and the remaining faces - lateral faces of the parallelepiped. The edges of the parallelepiped that do not belong to the bases are lateral ribs.

2 faces of a parallelepiped that have a common edge are adjacent, and those that do not have common edges - opposite.

A segment that connects 2 vertices that do not belong to the 1st face is parallelepiped diagonal.

The lengths of the edges of a rectangular parallelepiped that are not parallel are linear dimensions (measurements) parallelepiped. A rectangular parallelepiped has 3 linear dimensions.

Types of parallelepiped.

There are several types of parallelepipeds:

Direct is a parallelepiped with an edge perpendicular to the plane of the base.

A rectangular parallelepiped in which all 3 dimensions are equal is cube. Each of the faces of the cube is equal squares .

Any parallelepiped. The volume and ratios in an inclined parallelepiped are mainly determined using vector algebra. The volume of a parallelepiped is equal to the absolute value of the mixed product of 3 vectors, which are determined by the 3 sides of the parallelepiped (which originate from the same vertex). The relationship between the lengths of the sides of the parallelepiped and the angles between them shows the statement that the Gram determinant of the given 3 vectors is equal to the square of their mixed product.

Properties of a parallelepiped.

The parallelepiped is symmetrical about the middle of its diagonal.
Any segment with ends that belong to the surface of a parallelepiped and which passes through the middle of its diagonal is divided by it into two equal parts. All diagonals of the parallelepiped intersect at the 1st point and are divided by it into two equal parts.
The opposite faces of the parallelepiped are parallel and have equal dimensions.
The square of the length of the diagonal of a rectangular parallelepiped is equal to

Rectangular parallelepiped

A rectangular parallelepiped is a right parallelepiped whose all faces are rectangles.

It is enough to look around us, and we will see that the objects around us have a shape similar to a parallelepiped. They can be distinguished by color, have a lot of additional details, but if these subtleties are discarded, then we can say that, for example, a cabinet, box, etc., have approximately the same shape.

We come across the concept of a rectangular parallelepiped almost every day! Look around and tell me where you see rectangular parallelepipeds? Look at the book, it's exactly the same shape! A brick, a matchbox, a block of wood have the same shape, and even right now you are inside a rectangular parallelepiped, because the classroom is the brightest interpretation of this geometric figure.

Exercise: What examples of parallelepiped can you name?

Let's take a closer look at the cuboid. And what do we see?

First, we see that this figure is formed from six rectangles, which are the faces of a cuboid;

Secondly, a cuboid has eight vertices and twelve edges. The edges of a cuboid are the sides of its faces, and the vertices of the cuboid are the vertices of the faces.

Exercise:

1. What is the name of each of the faces of a rectangular parallelepiped? 2. Thanks to what parameters can a parallelogram be measured? 3. Define opposite faces.

Types of parallelepipeds

But parallelepipeds are not only rectangular, but they can also be straight and inclined, and straight lines are divided into rectangular, non-rectangular and cubes.

Assignment: Look at the picture and say what parallelepipeds are shown on it. How does a rectangular parallelepiped differ from a cube?

Properties of a rectangular parallelepiped

A rectangular parallelepiped has a number of important properties:

Firstly, the square of the diagonal of this geometric figure is equal to the sum of the squares of its three main parameters: height, width and length.

Secondly, all four of its diagonals are absolutely identical.

Thirdly, if all three parameters of a parallelepiped are the same, that is, the length, width and height are equal, then such a parallelepiped is called a cube, and all its faces will be equal to the same square.

Exercise

1. Does a rectangular parallelepiped have equal sides? If there are any, then show them in the figure. 2. What geometric shapes do the faces of a rectangular parallelepiped consist of? 3. What is the arrangement of equal edges in relation to each other? 4. Name the number of pairs of equal faces of this figure. 5. Find the edges in a rectangular parallelepiped that indicate its length, width, height. How many did you count?

Task

To beautifully decorate a birthday present for her mother, Tanya took a box in the shape of a rectangular parallelepiped. The size of this box is 25cm*35cm*45cm. To make this packaging beautiful, Tanya decided to cover it with beautiful paper, the cost of which is 3 hryvnia per 1 dm2. How much money should you spend on wrapping paper?

Do you know that the famous illusionist David Blaine spent 44 days in a glass parallelepiped suspended over the Thames as part of an experiment. For these 44 days he did not eat, but only drank water. In his voluntary prison, David took only writing materials, a pillow and mattress, and handkerchiefs.

The prism is called parallelepiped, if its bases are parallelograms. Cm. Fig.1.

Properties of a parallelepiped:

The opposite faces of a parallelepiped are parallel (that is, they lie in parallel planes) and equal.

The diagonals of a parallelepiped intersect at one point and are bisected by this point.

Adjacent faces of a parallelepiped– two faces that have a common edge.

Opposite faces of a parallelepiped– faces that do not have common edges.

Opposite vertices of a parallelepiped– two vertices that do not belong to the same face.

Diagonal of a parallelepiped– a segment that connects opposite vertices.

If the lateral edges are perpendicular to the planes of the bases, then the parallelepiped is called direct.

A right parallelepiped whose bases are rectangles is called rectangular. A prism, all of whose faces are squares, is called cube.

Parallelepiped- a prism whose bases are parallelograms.

Right parallelepiped- a parallelepiped whose lateral edges are perpendicular to the plane of the base.

Rectangular parallelepiped is a right parallelepiped whose bases are rectangles.

Cube– a rectangular parallelepiped with equal edges.

parallelepiped called a prism whose base is a parallelogram; Thus, a parallelepiped has six faces and all of them are parallelograms.

Opposite faces are pairwise equal and parallel. The parallelepiped has four diagonals; they all intersect at one point and are divided in half at it. Any face can be taken as a base; the volume is equal to the product of the area of the base and the height: V = Sh.

A parallelepiped whose four lateral faces are rectangles is called a straight parallelepiped.

A right parallelepiped whose six faces are rectangles is called rectangular. Cm. Fig.2.

The volume (V) of a right parallelepiped is equal to the product of the base area (S) and the height (h): V = Sh .

For a rectangular parallelepiped, in addition, the formula holds V=abc, where a,b,c are edges.

The diagonal (d) of a rectangular parallelepiped is related to its edges by the relation d 2 = a 2 + b 2 + c 2 .

Rectangular parallelepiped- a parallelepiped whose side edges are perpendicular to the bases, and the bases are rectangles.

Properties of a rectangular parallelepiped:

In a rectangular parallelepiped, all six faces are rectangles.

All dihedral angles of a rectangular parallelepiped are right.

The square of the diagonal of a rectangular parallelepiped is equal to the sum of the squares of its three dimensions (the lengths of three edges having a common vertex).

The diagonals of a rectangular parallelepiped are equal.

A rectangular parallelepiped, all of whose faces are squares, is called a cube. All edges of the cube are equal; the volume (V) of a cube is expressed by the formula V=a 3, where a is the edge of the cube.