The maximum guaranteed win of player a is called. Payment matrix
Let's consider the steam room the end game. Let the player A has m personal strategies, which we denote A 1 , A 2 , …,A m . Let the player IN available n personal strategies, let's designate them IN 1 ,IN 2 , …, IN n. They say the game of names is dimension mn. As a result of the players choosing any pair of strategies
A i And B i (I = 1, 2, …, m; j = 1, 2, …, n)
the outcome of the game is clearly determined, i.e., winning a ij player A(positive or negative) and loss (- a ij) player IN. Let's assume that the values a ij known for any pair of strategies ( Ai,Bj). Matrix R = (A ij), i = 1, 2, …, m; j = 1, 2, …, n, the elements of which are the winnings corresponding to the strategies A i And B j, called payment matrix or matrix of the game. General form such a matrix is presented in table. 1. The rows of this table correspond to the player’s strategies A, and the columns are the player’s strategies IN.
Let's create a payout matrix for the next game.
Table 1
|
A j B i |
||||
|
a 1n |
||||
|
a 2n |
||||
|
a m 1 |
a mn |
1. Search game.
Player A can hide in one of the shelters (I and II); player IN looking for a player A, and if found, he receives a fine of 1 den. units from A, otherwise pays the player A 1 day units It is necessary to build a payment matrix for the game.
Solution. To compile a payment matrix, you should analyze the behavior of each player. Player A can hide in shelter I - we denote this strategy by A 1 or to the shelter II - strategy A 2 .
Player IN can look for the first player in the shelter I - strategy IN 1, or in the shelter II - strategy IN 2. If the player A is located in Vault I and is discovered by the player there IN, i.e. a couple of strategies are implemented ( A 1 , IN 1), then the player A pays a fine, i.e. A 11 = -1. similarly we get A 22 = -1 (A 2 , IN 2). It is obvious that the strategies ( A 1 , IN 1) and ( A 2 , IN 2) give to the player A payoff is 1, so A 12 = A 21 = 1.
Start of the problem condition; - completion of the problem solution.
Thus, for a “search” game of size 2 2 we obtain the payoff matrix
Consider the game m n with matrix P = ( A ij), i = 1, 2, …, m; j = 1, 2, …, n and determine the best among strategies A 1 , A 2 , …, A m. Choosing a strategy A i, player A must expect that the player IN will answer it using one of the strategies B j , for which the payoff for the player A minimal (player IN seeks to “harm” the player A).
Let us denote by A i player's smallest winnings A when choosing a strategy A i for all possible player strategies IN(smallest number in i-th line of the payment matrix), i.e.
A ij = i . (1.1)
among all the numbers? i (i = 1, 2, …, m) choose the largest: ? = ? i. Shall we call it? lower price of the game, or maximum winnings (maximin). This is the guaranteed win of player A for any player strategy IN. Hence,
? = a ij . (1.2)
The strategy corresponding to maximin is called maximin strategy. Player IN interested in reducing the player's winnings A; choosing a strategy B j, it takes into account the maximum possible gain for A. Let's denote
? j = a ij (1.3)
Among all the numbers? j Shall we choose the smallest? = ? j and let's call it? top price of the game or minimax win (minimax). This is a guaranteed loss for the player IN. Hence,
? = a ij . (1.4)
The strategy corresponding to minimax is called minimax strategy.
The principle that dictates players to choose the most “cautious” minimax and maximin strategies is called the minimax principle. This principle follows from the reasonable assumption that each player strives to achieve a goal opposite to that of his opponent. Let us determine the lower and upper prices of the game and the corresponding strategies in the problem 1. Consider the payment matrix
from the problem 1. When choosing a strategy A 1 (first row of the matrix) the minimum winning is? 1 = min(-1;1) = -1 and corresponds to the strategy? 1 player IN. When choosing a strategy A 2 (second row of the matrix) the minimum winning is? 2 = min(1;-1) = -1, it is achieved with the strategy IN 2 .
Guaranteeing yourself maximum win for any player strategy IN, i.e. lower price for the game? = max(? 1 , ? 2) = max(-1,-1) = -1, player A can choose any strategy: A 1 or A 2, i.e. any of his strategies is maximin.
Choosing a strategy IN 1 (column 1), player IN understands that the player A will respond with a strategy A 2 to maximize your winnings (loss IN). Therefore, the player's maximum loss is IN when choosing a strategy IN Is 1 equal? 1 = max(-1;1) = 1.
Similarly, the maximum loss of a player IN(winning A) when choosing a strategy IN 2 (column 2) equals? 2 = max(1;-1) = 1.
Thus, for any player strategy A guaranteed minimum player loss IN equal? = min (? 1 ; ? 2) = min(1;1) = 1 - top price games.
Any player strategy IN is minimax. Having added the table 1 line? j and column? i, we get table. 2. At the intersection of the additional rows and columns, we will write down the upper and lower prices of the games.
Table 2.
|
A j B i |
? i |
||
|
? j |
In the problem 1 , discussed above, are the upper and lower prices of the game different? ? ?.
If the upper and lower prices of the game coincide, then general meaning top and lower price games? = ? = v is called clean at the cost of the game, or at the cost of the game. Minimax strategies corresponding to the price of the game are optimal strategies, and their totality is optimal decision, or decision games. In this case the player A receives the maximum guaranteed (independent of the player’s behavior) IN) payoff v, and the player IN achieves the minimum guaranteed (regardless of the player’s behavior A) loss v. They say that the solution of the game is stable, i.e. if one of the players sticks to his optimal strategy, then it cannot be profitable for the other to deviate from his optimal strategy.
Pair pure strategies A j And B i gives an optimal solution to the game if and only if the corresponding element a ij is both the largest in its column and the smallest in its row. This situation, if oan exists, is called saddle point(similar to the surface of a saddle, which curves up in one direction and down in the other).
Let's denote A * And B * - a pair of pure strategies that achieve a solution to the game in the problem with a saddle point. Let us introduce the payoff function of the first player for each pair of strategies: R(A i , B j) = a ij. Then from the optimality condition in saddle point the double inequality holds: R(A i , B *) ? R(A * , B * ) ? R(A * , B j), which is true for everyone i = 1, …, m; j = 1, …, n. indeed, the choice of strategy A * the first player with the optimal strategy B * the second player maximizes the minimum possible gain: R(A * , B * ) ? R(A * , B).
2. determine the lower and upper price of the game given by the payment matrix
P = 0.9 0.7 0.8
Table 3.
|
A i B j |
||||
Does the game have a saddle point?
Solution. It is convenient to carry out all calculations in a table, to which, in addition to the matrix P, a column is entered? i and line? j(Table 3). Analyzing the rows of the matrix (player strategies A), fill out the column? i: ? 1 = 0.5, ? 2 = 0.7, ? 3 = 0.6 - minimum numbers in lines 1, 2, 3. Similarly? 1 = 0.9, ? 2 = 0.7, ? 3 = 0.8 - maximum numbers in columns 1, 2, 3 respectively.
Lowest game price? = ? i= max (0.5; 0.7; 0.6) = 0.7 ( greatest number in column ? i) and the top price of the game? = ? j= min(0.9, 0.7, 0.8) = 0.7 (smallest number in the line? j). These values are equal, i.e. ? = ?, and are achieved using the same pair of strategies ( A 2 , IN 2). Therefore, the game has a saddle point ( A 2 , IN 2) and game price = 0.7.
A zero-sum game in which each player has a finite set of strategies at his disposal. The rules of the matrix game are determined by the payment matrix, the elements of which are the winnings of the first player, which are also the losses of the second player.
Matrix game is an antagonistic game. The first player receives the maximum guaranteed (independent of the behavior of the second player) winnings, equal to the price of the game; similarly, the second player achieves the minimum guaranteed loss.
Under strategy is understood as a set of rules (principles) that determine the choice of action for each personal move of the player, depending on the current situation.
Now about everything in order and in detail.
Payment matrix, pure strategies, game price
IN matrix game its rules are determined payment matrix .
Consider a game in which there are two participants: the first player and the second player. Let the first player have at his disposal m pure strategies, and at the disposal of the second player - n pure strategies. Since the game is being considered, it is natural that in this game there are wins and there are losses.
IN payment matrix the elements are numbers expressing the players' wins and losses. Wins and losses can be expressed in points, amount of money or other units.
Let's create a payment matrix:
If the first player chooses i-th pure strategy, and the second player - j th pure strategy, then the payoff of the first player will be aij units, and the loss of the second player is also aij units.
Because aij + (- a ij) = 0, then the described game is a zero-sum matrix game.
The simplest example of a matrix game is coin toss. The rules of the game are as follows. The first and second players throw a coin and the result is either heads or tails. If "heads" and "heads" or "tails" or "tails" are thrown at the same time, then the first player will win one unit, and in other cases he will lose one unit (the second player will win one unit). The same two strategies are at the disposal of the second player. The corresponding payment matrix will be as follows:
The task of game theory is to determine the choice of the first player's strategy, which would guarantee him the maximum average win, as well as the choice of the second player's strategy, which would guarantee him the maximum average loss.
How do you choose a strategy in a matrix game?
Let's look at the payment matrix again:
First, let's determine the amount of winnings for the first player if he uses i th pure strategy. If the first player uses i th pure strategy, then it is logical to assume that the second player will use such a pure strategy due to which the first player’s payoff would be minimal. In turn, the first player will use such a pure strategy that would provide him with the maximum win. Based on these conditions, the winnings of the first player, which we denote as v1 , called maximin winnings or lower price of the game .
At for these values, the first player should proceed as follows. From each line, write down the value of the minimum element and select the maximum one from them. Thus, the first player's winnings will be the maximum of the minimum. Hence the name - maximin winning. The line number of this element will be the number of the pure strategy that the first player chooses.
Now let’s determine the amount of loss for the second player if he uses j th strategy. In this case, the first player uses his own pure strategy in which the loss of the second player would be maximum. The second player must choose a pure strategy in which his loss would be minimal. The loss of the second player, which we denote as v2 , called minimax loss or top price of the game .
At solving problems on the price of the game and determining the strategy To determine these values for the second player, proceed as follows. From each column, write down the value of the maximum element and select the minimum from them. Thus, the loss of the second player will be the minimum of the maximum. Hence the name - minimax win. The column number of this element will be the number of the pure strategy that the second player chooses. If the second player uses "minimax", then regardless of the choice of strategy by the first player, he will lose no more than v2 units.
Example 1.
 .
.

The largest of the smallest elements of the rows is 2, this is the lower price of the game, the first row corresponds to it, therefore, the maximin strategy of the first player is the first. The smallest of the largest elements of the columns is 5, this is the upper price of the game, the second column corresponds to it, therefore, the minimax strategy of the second player is the second.
Now that we have learned to find the lower and upper price of the game, the maximin and minimax strategies, it’s time to learn how to formally define these concepts.
So, the guaranteed win for the first player is:
The first player must choose a pure strategy that would provide him with the maximum of the minimum winnings. This gain (maximin) is denoted as follows:
![]() .
.
The first player uses his pure strategy so that the loss of the second player is maximum. This loss is indicated as follows:
The second player must choose his pure strategy so that his loss is minimal. This loss (minimax) is indicated as follows:
![]() .
.
Another example from the same series.
Example 2. Given a matrix game with a payoff matrix
 .
.
Determine the maximin strategy of the first player, the minimax strategy of the second player, the lower and upper price of the game.
Solution. To the right of the payment matrix, we will write out the smallest elements in its rows and note the maximum of them, and below the matrix - the largest elements in the columns and select the minimum of them:

The largest of the smallest elements of the lines is 3, this is the lower price of the game, the second line corresponds to it, therefore, the maximin strategy of the first player is the second. The smallest of the largest elements of the columns is 5, this is the upper price of the game, the first column corresponds to it, therefore, the minimax strategy of the second player is the first.
Saddle point in matrix games
If the upper and lower prices of the game are the same, then the matrix game is considered to have a saddle point. The converse is also true: if a matrix game has a saddle point, then the upper and lower prices of the matrix game are the same. The corresponding element is both the smallest in the row and the largest in the column and is equal to the price of the game.
Thus, if , then is the optimal pure strategy of the first player, and is the optimal pure strategy of the second player. That is, equal lower and upper game prices are achieved using the same pair of strategies.
In this case matrix game has a solution in pure strategies .
Example 3. Given a matrix game with a payoff matrix
 .
.
Solution. To the right of the payment matrix, we will write out the smallest elements in its rows and note the maximum of them, and below the matrix - the largest elements in the columns and select the minimum of them:
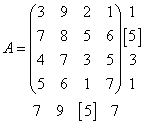
The lower price of the game coincides with the upper price of the game. Thus, the price of the game is 5. That is . The price of the game is equal to the value of the saddle point. The first player's maxin strategy is the second pure strategy, and the second player's minimax strategy is the third pure strategy. This matrix game has a solution in pure strategies.
Solve a matrix game problem yourself, and then look at the solution
Example 4. Given a matrix game with a payoff matrix
 .
.
Find the lower and upper price of the game. Does this matrix game have a saddle point?
Matrix games with optimal mixed strategy
In most cases, a matrix game does not have a saddle point, so the corresponding matrix game has no solutions in pure strategies.
But she has a solution in optimal mixed strategies. To find them, you need to assume that the game is repeated a sufficient number of times so that, based on experience, you can guess which strategy is more preferable. Therefore, the decision is associated with the concept of probability and average (mathematical expectation). In the final solution there is both an analogue of the saddle point (that is, the equality of the lower and upper prices of the game), and an analogue of the strategies corresponding to them.
So, in order for the first player to get the maximum average win and for the second player to have a minimum average loss, pure strategies should be used with a certain probability.
If the first player uses pure strategies with probabilities ![]() , then the vector
, then the vector ![]() is called a mixed first player strategy. In other words, it is a “mixture” of pure strategies. In this case, the sum of these probabilities is equal to one:
is called a mixed first player strategy. In other words, it is a “mixture” of pure strategies. In this case, the sum of these probabilities is equal to one:
![]() .
.
If the second player uses pure strategies with probabilities ![]() , then the vector
, then the vector ![]() is called a second player mixed strategy. In this case, the sum of these probabilities is equal to one:
is called a second player mixed strategy. In this case, the sum of these probabilities is equal to one:
![]() .
.
If the first player uses a mixed strategy p, and the second player - a mixed strategy q, then it makes sense expected value the first player's win (the second player's loss). To find it, you need to multiply the first player's mixed strategy vector (which will be a one-row matrix), the payoff matrix and the second player's mixed strategy vector (which will be a one-column matrix):
![]() .
.
Example 5. Given a matrix game with a payoff matrix
![]() .
.
Determine the mathematical expectation of the first player's win (the second player's loss), if the first player's mixed strategy is , and the second player's mixed strategy is .
Solution. According to the formula for the mathematical expectation of the first player’s win (the second player’s loss), it is equal to the product of the first player’s mixed strategy vector, the payment matrix and the second player’s mixed strategy vector:

The first player is called such a mixed strategy that would provide him with the maximum average payoff if the game is repeated a sufficient number of times.
Optimal mixed strategy the second player is called such a mixed strategy that would provide him with a minimum average loss if the game is repeated a sufficient number of times.
By analogy with the notation of maximin and minimax in the case of pure strategies, optimal mixed strategies are denoted as follows (and are associated with mathematical expectation, that is, the average of the winnings of the first player and the losses of the second player):
![]() ,
,
![]() .
.
In this case, for the function E there is a saddle point , which means equality.
In order to find optimal mixed strategies and a saddle point, that is, solve a matrix game in mixed strategies , we need to reduce the matrix game to the problem linear programming, that is, to an optimization problem, and solve the corresponding linear programming problem.
Reducing a matrix game to a linear programming problem
In order to solve a matrix game in mixed strategies, you need to construct a straight line linear programming problem And dual task. In the dual problem, the extended matrix, which stores the coefficients of the variables in the system of constraints, free terms and coefficients of the variables in the objective function, is transposed. In this case, the minimum of the goal function of the original problem is matched to the maximum in the dual problem.
Goal function in a direct linear programming problem:
![]() .
.
System of constraints in a direct linear programming problem:
![]()
The goal function in the dual problem is:
![]() .
.
System of restrictions in the dual problem:
![]()
The optimal plan for a direct linear programming problem is denoted by
![]() ,
,
and the optimal plan for the dual problem is denoted by
We denote the linear forms for the corresponding optimal plans by and ,
and they need to be found as sums of the corresponding coordinates of optimal plans.
In accordance with the definitions of the previous paragraph and the coordinates of optimal plans, the following mixed strategies of the first and second players are valid:
![]() .
.
Theoretical mathematicians have proven that game price is expressed in the following way through the linear forms of optimal plans:
![]() ,
,
that is, it is the reciprocal of the sums of coordinates of optimal plans.
We, practitioners, can only use this formula to solve matrix games in mixed strategies. Like formulas for finding optimal mixed strategies the first and second players respectively:
in which the second factors are vectors. Optimal mixed strategies are also, as we already defined in the previous paragraph, vectors. Therefore, multiplying the number (game price) by a vector (with the coordinates of optimal plans) we also obtain a vector.
Example 6. Given a matrix game with a payoff matrix
 .
.
Find the price of the game V and optimal mixed strategies and .
Solution. We create a linear programming problem corresponding to this matrix game:

We obtain a solution to the direct problem:
![]() .
.
We find the linear form of the optimal plans as the sum of the found coordinates.
Consider a game with a matrix

The letter i will denote the number of our strategy, and the letter the number of the enemy’s strategy.
Let's discard the question of mixed strategies and consider only pure ones for now. Let's set the task: to determine the best among our strategies. Let's analyze each of them sequentially, starting with and ending with. When choosing, we must expect that the enemy will respond to it with the strategy for which our winnings are minimal. Let's find the smallest number in the line and denote it
![]()
(the sign indicates the minimum value of this parameter for all possible
Let's write down the numbers (row minimums) next to the matrix on the right in the form of an additional column:

When choosing a strategy, we must count on the fact that as a result of the enemy’s reasonable actions we will only win. Naturally, acting most carefully (i.e., avoiding any risk), we must prefer to others the strategy for which the number is maximum. Let's denote this maximum value
or. taking into account formula (4.1),
![]()
The value a is called the lower price of the game, otherwise the maximin payoff or maximin. The strategy of player A that corresponds to maximin a is called maximin strategy.
Obviously, if we adhere to the maximin strategy, then regardless of the enemy’s behavior we are guaranteed a win, at least not less than a. Therefore, the value a is called the “lower price of the game.” This is the guaranteed minimum that we can provide for ourselves by adhering to our most cautious (“reinsurance”) strategy.
Obviously, a similar reasoning can be carried out for opponent B. He is interested in reducing our winnings to a minimum; this means that he must look through all his strategies, highlighting the maximum winning value for each of them. Let us write down the matrix (4.2) maximum values by columns:
![]()
and find their minimum:
![]() (4.4)
(4.4)
The value is called the upper price of the game, otherwise the minimax win or minimax. The opponent's winning strategy is called his minimax strategy. By sticking to his most cautious minimax strategy, the opponent is guaranteed that in any case he will lose no more than p.
The principle of caution, which dictates that players choose appropriate strategies (maximin and minimax), is fundamental in game theory and is called the minimax principle. It follows from the assumption that each player is reasonable, striving to achieve a goal opposite to the opponent’s goal. The most “cautious” maximin and minimax strategies are often denoted general term"minimax strategies".
Let us determine the lower and upper prices of the game, as well as minimax strategies, for the three examples discussed in the previous paragraph.
Example 1. (Search game). Determining the row minima and column maxima we get

Since the values , are constant and equal to -1, respectively, and the lower and upper prices of the game are also equal to -1 and
Any strategy of player A is his maximin strategy, and any strategy of player B is his minimax strategy. The conclusion is trivial: by adhering to any of his strategies, player A can guarantee that he will lose no more than 1 ruble; Player B can guarantee the same for any of his strategies.
Example 2. (Three fingers game). By writing out the minimums of the rows and maximums of the columns, we will find the lower price of the game and the upper one (highlighted in bold in the table). Our maximin strategy (by applying it systematically, we guarantee that we will win no less than -3, i.e. we will lose no more than 3).

The enemy’s minimax strategy is any of the strategies, using them systematically, he can guarantee that he will not give up more than 4. If we deviate from our maximin strategy (for example, choose A 2), then the enemy can “punish” us for this by applying and reducing our winning and the opponent's retreat from his minimax strategy can be “punished” by increasing his loss to 6.
Let us pay attention to the fact that minimax strategies in in this case not stable. Indeed, let, for example, the opponent choose one of his minimax strategies and stick to it. Having learned this, we will move on to strategy and win 4. The enemy will respond with strategy and win 5; to this we, in turn, will respond with a strategy and win 4, etc. Thus, the situation in which both players use their minimax strategies is unstable and can be violated by the received information about the strategy used by the other side. However, such instability is not always observed; We will see this in the following example.
Example 3. (Game “weapons and aircraft”). Determine row minimums and column maximums:

In this case, the lower price of the game is equal to the upper:
![]()
Minimax strategies are stable: if one of the players adheres to his minimax (maximin) strategy, then the other player cannot improve his position by deviating from his.
Thus, we see that there are games for which the lower price is equal to the upper:
These games occupy a special place in game theory and are called saddle point games. In the matrix of such a game there is an element that is both minimal in its row and maximal in its column; such an element is called a saddle point” (by analogy with a saddle point on a surface, where a minimum is achieved along one coordinate and a maximum along another).
The total value of the lower and upper price of the game
called the net price of the game.
The saddle point corresponds to a pair of minimax strategies; these strategies are called optimal, and their combination is called a solution to the game. The solution of the game has the following property: if one of the players adheres to his optimal strategy, then it cannot be profitable for the other to deviate from his optimal one (such a deviation will either leave the situation unchanged or worsen it).
Indeed, in a game with a saddle point, let player A stick to his optimal strategy, and player B stick to his. As long as this is so, the payoff remains constant and equal to the game price v. Now suppose that B deviated from his optimal strategy. Since v is the minimum element in its row, such a deviation cannot be beneficial to B; Likewise, for A, if B adheres to his optimal strategy, deviation from his cannot be beneficial.
We see that for a game with a saddle point, minimax strategies are stable. A pair of optimal strategies in a game with a saddle point is like an equilibrium position: a deviation from the optimal strategy causes a change in the payoff that is disadvantageous for the deviating player and forces him to return to his optimal strategy.
The net price of play v in a saddle point game is the value of the payoff that, in a game against a reasonable opponent, player A cannot increase and player B cannot decrease.
Note that there may be more than one saddle point in the payment matrix, but several.

For example, there are six saddle points in the matrix, with a common payoff value and corresponding pairs of optimal strategies: It is not difficult to prove (we will not do this) that if there are several saddle points in the game matrix, then they all give the same payoff value.

Example. Side A - air defense systems - defends a section of territory from an air raid, having two guns No. 1 and No. 2, the coverage areas of which do not overlap (Fig. 9.1). Each weapon can only fire at an aircraft passing through its coverage area, but to do this it must track it in advance (before the target enters the area) and generate targeting data. If the target is fired at, it is hit with a probability. Side B has two aircraft, each of which can be directed to any zone At the moment when side A carries out target distribution (assigns which weapon to shoot at which target), the movement of target aircraft No. 1 is directed into the range of action of gun No. 1, and target No. 2 is directed into the range of action of gun No. 2 However, after making a decision on target distribution, each target can maneuver using a “deception maneuver” (see dotted arrows in Figure 9.1).
The task of side A is to maximize, and side B’s task is to minimize the number of targets hit. Find a solution to the game (optimal strategies of the parties)
Solution. Side A (air defense weapons) has four possible strategies - each gun monitors the target heading into its zone,
The guns track targets “crosswise” (each one tracking a target heading towards its neighbor),
Both guns are tracking target No. 1,
Both guns are tracking target No. 2. Side B (target aircraft) also has four strategies:
Both intact do not change direction,
Both targets use deception.
The first target uses a deception maneuver, but the second does not,
The second target uses a deception maneuver, but the first does not.
The result is a 4X4 game, the matrix of which is given in the table:

By finding the minima of the rows and the maxima of the columns, we are convinced that the lower price of the game is equal to the upper price of the game: this means that the game has a saddle point and a solution in pure strategies, leading to the net price of the game. In this case, there is not one, but four saddle points. Each of them corresponds to a pair of optimal strategies that give a solution to the game. The price of the game means that with optimal behavior of the parties, the planes will inevitably lose one plane, and no tricks will help them lose less, and the means Air defense - shoot down more than one aircraft This state of equilibrium is achieved when both sides use their optimal strategies: both guns track the same aircraft (any), and the aircraft are sent after target distribution to the same zone (any)
The class of games that have a saddle point is very interesting from both theoretical and practical points of view. It includes, in particular, all the so-called “games with complete information».
A game with complete information is a game in which each player, with each personal move, knows the results of all previous moves - both personal and random. Examples of games with complete information include: checkers, chess, famous game in “tacs and toes”, etc.
In game theory it is proven that every game with complete information has a saddle point and, therefore, a solution in pure strategies. In other words, in every game with complete information, there is a pair of optimal strategies on both sides that give a stable payoff equal to the net cost of the game. If a game with complete information consists only of personal moves, then when each side applies its optimal strategy, the game should always end with a well-defined outcome equal to the cost of the game
As an example, consider the following game with complete information. Two players alternately place identical coins on round table, choosing the position of the coin arbitrarily (mutual overlap of coins is not allowed). The winner is the one who puts in the last coin (when there is no room left for others). It is not difficult to see that the outcome of this game is predetermined, and there is a certain strategy that ensures a certain win for the player who puts in the coin first. Namely, he must place the coin in the center of the table for the first time, and then respond to each opponent’s move with a symmetrical move. Obviously, no matter how the enemy behaves, he cannot avoid losing. Therefore, the game makes sense only for people who do not know its solution. The situation is exactly the same with chess and other games with complete information; any of these games has a saddle point and, therefore, a solution that indicates to each player his optimal strategy, so the game makes sense only as long as the solution is unknown. A solution to the chess game has not been found (and is unlikely to be found in the foreseeable future) only because the number of strategies (combinations of moves) in chess is too large to be able to construct a payoff matrix and find a saddle point in it.
PRACTICAL WORK No. 3
Game theory models
The concept of gaming models
Game theory deals with the development of various kinds of recommendations for making decisions in a conflict situation. Forming conflict situations mathematically, they can be represented as a game of two, three or more players, each of whom pursues the goal of maximizing their winnings at the expense of the other player. The mathematical model of a conflict situation is called game, the parties involved in the conflict – players, and the outcome of the conflict is win. For each formalized game, rules, i.e. system of conditions defining:
1. options for players’ actions;
2. the amount of information each player has about the behavior of their partners;
3. the gain that each set of actions leads to.
As a rule, the winnings can be specified quantitatively (for example, a loss is 0, a win is 1, a draw is ½). The game is called steam room, if it involves two players, and multiple, if the number of players is more than two. The game is called zero sum game, if the gain of one of the players is equal to the loss of the other. The choice and implementation of one of the actions provided for by the rules is called progress player. Moves can be personal and random. Personal move– a conscious choice by the player of one of the possible actions (a move in chess game), random move– a randomly selected action (choosing a card from a shuffled deck).
Player strategy is a set of rules that determine the choice of his action for each personal move, depending on the current situation. The game is called ultimate, if the player has a finite number of strategies, and endless- otherwise.
To solve a game, or find game solution, you should choose a strategy for each player that satisfies the optimality condition, i.e. one of the players must receive maximum win when the second one sticks to his strategy. At the same time, the second player must have minimum loss, if the first one sticks to his strategy. Such strategies are called optimal. Purpose game theory is to determine the optimal strategy for each player. When choosing an optimal strategy, it is natural to assume that both players behave reasonably in terms of their interests.
Payment matrix. Lower and upper price of the game
Consider a paired finite game. Let the player A has m personal strategies, which we denote A 1, A 2,…, A m. Let the player B available n personal strategies, let's designate them B 1, B 2,…, B n. They say the game has dimensions m´n. As a result of the players choosing any pair of strategies A i And Bj The outcome of the game is clearly determined, i.e. winnings a ij player A(positive or negative) and loss (- a ij) player IN. Matrix Р=(a ij), the elements of which are the winnings corresponding to the strategies A i And Bj, called payment matrix or matrix of the game.
| Bj A i | B 1 | B 2 | … | Bn |
| A 1 | a 11 | a 12 | … | a 1n |
| A 2 | a 21 | a 22 | … | a 2n |
| … | … | … | … | … |
| Am | a m1 | am 2 | a mn |
Example - the game "Search"
Player A can hide in shelter 1 - let's denote this strategy as A 1 or in shelter 2 - strategy A 2. Player IN can look for the first player in hideout 1 – strategy IN 1, or in shelter 2 - strategy AT 2. If the player A is located in shelter 1 and is discovered there by the player IN, i.e. a couple of strategies are being implemented (A 1,B 1), then the player A pays a fine, i.e. a 11=–1. Similarly we get a 22=–1. It is obvious that the strategies (A 1,B 2) And (A 2,B 1) give to the player A payoff is 1, so a 12=a 21=1. Thus, we obtain the payment matrix
Consider the game m´n with matrix Р=(a ij) and determine the best among the player’s strategies A. Choosing a strategy A i, player A must expect that the player IN will answer it using one of the strategies In j, for which the payoff for the player A minimal (player IN seeks to “harm” the player A).
Let us denote by a i player's smallest winnings A when choosing a strategy A i for all possible player strategies IN(smallest number in i th line payment matrix), i.e. .
Among all the numbers a i Let's choose the largest: . Let's call a lower price of the game
, or maximum winnings
(maximin
). This guaranteed payoff of player A for any strategy of player B. Hence, ![]() .
.
The strategy corresponding to maximin is called maximin strategy. Player IN interested in reducing the player's winnings A; choosing a strategy Bj, it takes into account the maximum possible gain for A. Let us denote .
Among all the numbers, we choose the smallest one and call it b top price of the game
, or minimax win
(minimax
). This guaranteed loss of player B for any strategy of player A. Hence, ![]() .
.
The strategy corresponding to minimax is called minimax strategy. The principle that dictates that players choose the most cautious minimax and maximin strategies is called minimax principle.
In many tasks that lead to games, uncertainty is caused by the lack of information about the conditions under which the action is carried out. These conditions depend not on the conscious actions of the other player, but on objective reality, which is commonly called “nature.” Such games are called games with nature (statistical games).
Task
After several years of operation, industrial equipment finds itself in one of the following states: B 1 – the equipment can be used in next year after preventive maintenance; B 2 – for trouble-free operation of the equipment in the future, individual parts and assemblies should be replaced; 3 – equipment requires major repairs or replacement.
Depending on the current situation B 1, B 2, B 3, the management of the enterprise can make the following decisions: A 1 - repair the equipment by factory specialists, which requires corresponding costs a 1 = 6, and 2 = 10, and 3 = 15 monetary units ; A 2 - call a special team of repairmen, the costs in this case will be b 1 = 15, b 2 = 9, b 3 = 18 monetary units; A 3 – replace the equipment with new one, selling the obsolete equipment at its residual value. The total costs associated with the results of this event will be equal to, respectively, c 1 =13, c 2 =24, c 3 =12 monetary units.
Exercise
1. Having given the described situation game scheme, identify its participants, indicate possible pure strategies of the parties.
2. Create a payment matrix, explaining the meaning of the elements a ij of the matrix (why are they negative?).
3. Find out what decision on the operation of equipment in the coming year is advisable to recommend to the management of the enterprise in order to minimize losses under the following assumptions: a) the experience accumulated at the enterprise in operating similar equipment shows that the probabilities of the indicated equipment states are equal, respectively, q 1 = 0.15; q 2 =0.55; q 3 =0.3 (apply Bayes criterion); b) existing experience indicates that all three possible states of the equipment are equally probable (apply the Laplace criterion); c) nothing definite can be said about the probability of equipment (apply the Wald, Savage, Hurwitz criteria). The value of the parameter g=0.8 in the Hurwitz criterion is specified.
Solution
1) The described situation is a statistical game.
The statistician is the management of the enterprise, which can make one of the following decisions: repair the equipment on its own (strategy A 1), call repairmen (strategy A 2); replace the equipment with new ones (strategy A 3).
The second playing side, nature, will be considered a set of factors influencing the condition of the equipment: the equipment can be used after preventative repairs (condition B 1); individual components and parts of equipment need to be replaced (state B 2): major repairs or replacement of equipment will be required (state B 3).
2) Let’s create the payment matrix of the game:

Element of the payment matrix a ij shows the costs of the enterprise management if, with the chosen strategy A i, the equipment ends up in state B j. The elements of the payment matrix are negative, since with any chosen strategy, the management of the enterprise will have to bear costs.
a) the experience accumulated at the enterprise in operating similar equipment shows that the probabilities of equipment states are equal to q 1 = 0.15; q 2 =0.55; q 3 =0.3.
Let's present the payment matrix as:
| Strategies statistics, A i | States of nature B j | |||
| B 1 | B 2 | B 3 | ||
| A 1 | -6 | -10 | -15 | -10,9 |
| A 2 | -15 | -9 | -18 | -12,6 |
| A 3 | -13 | -24 | -12 | -18,75 |
| q j | 0,15 | 0,55 | 0,3 |
where , (i=1.3)
According to the Bayes criterion, the optimal pure strategy A i is taken to be the one that maximizes the average gain of the statistician, i.e. provided =max .
The optimal strategy according to Bayes is strategy A 1 .
b) existing experience indicates that all three possible states of the equipment are equally probable, i.e. = 1/3.
Average winnings are:
1/3*(-6-10-15) = -31/3 "-10.33;
1/3*(-15-9-18) = -42/3 = -14;
1/3*(-13-24-12) = -49/3 » -16.33.
The optimal Laplace strategy is strategy A 1 .
c) nothing definite can be said about the probabilities of equipment.
According to the Wald criterion, a pure strategy is taken as optimal, which under the worst conditions guarantees the maximum gain, i.e.
![]() .
.
![]() = max (-15, -18, -24) = -15.
= max (-15, -18, -24) = -15.
Thus, strategy A 1 is optimal.
Let's build a risk matrix, where .
Consider a paired finite game. Let the player A has T personal strategies, which we denote
Let the player IN available P personal strategies, let us designate them. They say the game has dimensions T X P.
As a result of the players’ choice of any pair of strategies, the outcome of the game is uniquely determined, i.e. winnings A;. player A(positive or negative) and loss (-ay) player IN. Let's assume that the values A.. known for any pair of strategies (A:, B;.). Matrix P =(a..), i = = 1, 2, ..., m j = 1, 2, ..., P, the elements of which are winnings corresponding to the strategies A. And Bj, called payment matrix, or matrix of the game. The general appearance of such a matrix is presented in Table. 12.1. The rows of this table correspond to the player's strategies A, and the columns – the player’s strategies IN.
Table 12.1
Let's create a payment matrix for the next game.
12.1. Search game.
Player A can hide in one of two shelters (I and II); player IN looking for a player A, and if he finds it, he receives a fine of 1 den. units from A, otherwise pays the player A 1 day units It is necessary to build the payment matrix of the game.
SOLUTION. To compile a payment matrix, you should analyze the behavior of each player. Player A can hide in shelter I - we denote this strategy by A v or to the shelter II – strategy A. d Player IN can look for the first player in the shelter I - strategy IN(or to the shelter II - strategy IN.,. If the player A is located in Vault I and is discovered by the player there IN, those. a couple of strategies are being implemented (Α ν IN{), then the player A pays a fine, i.e. A n = -1. Similarly we get A. n = -1 (A 2, IN.,). It is obvious that strategies (A, IN.,) and (L2, /1,) give the player A payoff is 1, so A P = a. n = I. Thus, for a search game of size 2x2, we obtain the payoff matrix:
Consider the game T X P with matrix P =a j) , i = 1,2, ..., τη; j= 1, 2, ..., and and determine the best among strategies A at A v..., A t. Choosing a strategy A jy player A must expect that the player IN will answer it using one of the strategies IN., for which the payoff for the player A minimal (player IN seeks to "harm" the player A).
Let us denote by a; player's smallest winnings A when he chooses strategy L; for all possible player strategies IN(smallest number in i-th line payment matrix), i.e.
Among all numbers a (r = 1,2,..., T) Let's choose the largest: . Let's call and the lower price of the game, or maximum winnings (maximin). This guaranteed win for player A for any strategy of player B. Hence,
![]() (12.2)
(12.2)
The strategy corresponding to maximin is called maximin strategy. Player IN interested in reducing the player's winnings A; choosing a strategy IN., it takes into account the maximum possible gain for A. Let's denote
Among all the numbers β. let's choose the smallest one,
and call β top price of the game, or minimax win (minimax). This guaranteed loss for player B. Hence,
![]() (12.4)
(12.4)
The strategy corresponding to minimax is called minimax strategy.
The principle that dictates that players choose the most “cautious” minimax and maximin strategies is called the principle minimax. This principle follows from the reasonable assumption that each player strives to achieve a goal opposite to that of his opponent. Let us determine the lower and upper prices of the game and the corresponding strategies in Problem 12.1. Consider the payment matrix
from problem 12.1. When choosing strategy L, (first row of the matrix), the minimum payoff is equal to a, =min(-l; 1) = -1 and corresponds to the player’s strategy β1 IN. When choosing a strategy L 2 (second row of the matrix) the minimum winning is A 2 = min(l; -1) = -1, it is achieved with the strategy IN.,.
Guaranteeing yourself the maximum win for any player strategy IN, i.e. lower price of the game a = max(a, a2) = = max(-l; -1) = -1, player A can choose any strategy: Aj or A 2, i.e. any of his strategies is maximin.
Choosing strategy B, (column 1), the player IN understands that the player A will respond with a strategy A 2 to maximize your winnings (losing IN). Therefore, the player's maximum loss is IN when he chooses strategy B, is equal to β, = check(-1; 1) = 1.
Similarly, the maximum loss of player B (win A) when he chooses strategy B2 (column 2) is equal to β2 = max(l; -1) = 1.
Thus, for any player strategy A the guaranteed minimum loss of player B is equal to β = = πιίη(β1, β2) = min(l; 1) = 1 - the upper price of the game.
Any strategy of player B is minimax. Having added the table 12.1 line β; and column a;, we get table. 12.2. At the intersection of the additional rows and columns we will write down the upper and lower prices of the games.
Table 12.2
In Problem 12.1 discussed above, the upper and lower prices of the game are different: a F β.
If the upper and lower prices of the game coincide, then the total value of the upper and lower prices of the game α = β = υ is called the pure price of the game, or at the cost of the game. Minimax strategies corresponding to the price of the game are optimal strategies, and their totality - the optimal solution, or decision games. In this case the player A receives the maximum guaranteed (independent of the player’s behavior) IN) the payoff is υ, and the player IN achieves the minimum guaranteed (regardless of the behavior of player A) loss υ. They say that the solution to the game has stability, those. If one player sticks to his optimal strategy, then it cannot be profitable for the other to deviate from his optimal strategy.
A couple of pure strategies A. and B. gives an optimal solution to the game if and only if the corresponding element y is simultaneously the largest in its column and the smallest in its row. This situation, if it exists, is called saddle point(similar to the surface of a saddle, which curves up in one direction and down in the other).
Let's denote A* And IN*– a pair of pure strategies that achieve a solution to the game in the saddle point problem. Let us introduce the payoff function of the first player for each pair of strategies: P(A:, IN-) = and y. Then, from the optimality condition at the saddle point, the double inequality holds: P(Aj, B*)<Р(А*, В*)<Р(А", В ), which is fair for everyone i = 1, 2, ..., m;j = 1, 2, ..., P. Indeed, the choice of strategy A* the first player with an optimal strategy IN" the second player maximizes the minimum possible payoff: P(A*, B")> P(A G IN"), and the choice of strategy B" the second player, with the optimal strategy of the first, minimizes the maximum loss: P(D, IN*)<Р(А", В).
12.2. Determine the lower and upper price of the game given by the payment matrix

Does the game have a saddle point?
Table 12. 3
Solution. It is convenient to carry out all calculations in a table, which, in addition to the matrix R, column a is entered; and string)




