How to find the average probability. Calculation of the probability of combining (logical sum) of events

Initially, being just a collection of information and empirical observations about the game of dice, the theory of probability became a thorough science. The first to give it a mathematical framework were Fermat and Pascal.

From thinking about the eternal to the theory of probability

The two individuals to whom probability theory owes many of its fundamental formulas, Blaise Pascal and Thomas Bayes, are known as deeply religious people, the latter being a Presbyterian minister. Apparently, the desire of these two scientists to prove the fallacy of the opinion about a certain Fortune giving good luck to her favorites gave impetus to research in this area. After all, in fact, any gambling game with its winnings and losses is just a symphony of mathematical principles.

Thanks to the passion of the Chevalier de Mere, who was equally a gambler and a man not indifferent to science, Pascal was forced to find a way to calculate probability. De Mere was interested in the following question: “How many times do you need to throw two dice in pairs so that the probability of getting 12 points exceeds 50%?” The second question, which was of great interest to the gentleman: “How to divide the bet between the participants in the unfinished game?” Of course, Pascal successfully answered both questions of de Mere, who became the unwitting initiator of the development of probability theory. It is interesting that the person of de Mere remained known in this area, and not in literature.

Previously, no mathematician had ever attempted to calculate the probabilities of events, since it was believed that this was only a guessing solution. Blaise Pascal gave the first definition of the probability of an event and showed that it is a specific figure that can be justified mathematically. Probability theory has become the basis for statistics and is widely used in modern science.

What is randomness

If we consider a test that can be repeated an infinite number of times, then we can define a random event. This is one of the likely outcomes of the experiment.

Experience is the implementation of specific actions under constant conditions.

To be able to work with the results of the experiment, events are usually designated by the letters A, B, C, D, E...

Probability of a random event

In order to begin the mathematical part of probability, it is necessary to define all its components.

The probability of an event is a numerical measure of the possibility of some event (A or B) occurring as a result of an experience. The probability is denoted as P(A) or P(B).

In probability theory they distinguish:

• reliable the event is guaranteed to occur as a result of the experience P(Ω) = 1;
• impossible the event can never happen P(Ø) = 0;
• random an event lies between reliable and impossible, that is, the probability of its occurrence is possible, but not guaranteed (the probability of a random event is always within the range 0≤Р(А)≤ 1).

Relationships between events

Both one and the sum of events A+B are considered, when the event is counted when at least one of the components, A or B, or both, A and B, is fulfilled.

In relation to each other, events can be:

• Equally possible.
• Compatible.
• Incompatible.
• Opposite (mutually exclusive).
• Dependent.

If two events can happen with equal probability, then they equally possible.

If the occurrence of event A does not reduce to zero the probability of the occurrence of event B, then they compatible.

If events A and B never occur simultaneously in the same experience, then they are called incompatible. Tossing a coin is a good example: the appearance of heads is automatically the non-appearance of heads.

The probability for the sum of such incompatible events consists of the sum of the probabilities of each of the events:

P(A+B)=P(A)+P(B)

If the occurrence of one event makes the occurrence of another impossible, then they are called opposite. Then one of them is designated as A, and the other - Ā (read as “not A”). The occurrence of event A means that Ā did not happen. These two events form a complete group with a sum of probabilities equal to 1.

Dependent events have mutual influence, decreasing or increasing the probability of each other.

Relationships between events. Examples

Using examples it is much easier to understand the principles of probability theory and combinations of events.

The experiment that will be carried out consists of taking balls out of a box, and the result of each experiment is an elementary outcome.

An event is one of the possible outcomes of an experiment - a red ball, a blue ball, a ball with number six, etc.

Test No. 1. There are 6 balls involved, three of which are blue with odd numbers on them, and the other three are red with even numbers.

Test No. 2. There are 6 blue balls with numbers from one to six.

Based on this example, we can name combinations:

• Reliable event. In Spanish No. 2 the event “get the blue ball” is reliable, since the probability of its occurrence is equal to 1, since all the balls are blue and there can be no miss. Whereas the event “get the ball with the number 1” is random.
• Impossible event. In Spanish No. 1 with blue and red balls, the event “getting the purple ball” is impossible, since the probability of its occurrence is 0.
• Equally possible events. In Spanish No. 1, the events “get the ball with the number 2” and “get the ball with the number 3” are equally possible, and the events “get the ball with an even number” and “get the ball with the number 2” have different probabilities.
• Compatible Events. Getting a six twice in a row while throwing a die is a compatible event.
• Incompatible events. In the same Spanish No. 1, the events “get a red ball” and “get a ball with an odd number” cannot be combined in the same experience.
• Opposite events. The most striking example of this is coin tossing, where drawing heads is equivalent to not drawing tails, and the sum of their probabilities is always 1 (full group).
• Dependent Events. So, in Spanish No. 1, you can set the goal of drawing the red ball twice in a row. Whether or not it is retrieved the first time affects the likelihood of being retrieved the second time.

It can be seen that the first event significantly affects the probability of the second (40% and 60%).

Event probability formula

The transition from fortune-telling to precise data occurs through the translation of the topic into a mathematical plane. That is, judgments about a random event such as “high probability” or “minimal probability” can be translated into specific numerical data. It is already permissible to evaluate, compare and enter such material into more complex calculations.

From a calculation point of view, determining the probability of an event is the ratio of the number of elementary positive outcomes to the number of all possible outcomes of experience regarding a specific event. Probability is denoted by P(A), where P stands for the word “probabilite”, which is translated from French as “probability”.

So, the formula for the probability of an event is:

Where m is the number of favorable outcomes for event A, n is the sum of all outcomes possible for this experience. In this case, the probability of an event always lies between 0 and 1:

0 ≤ P(A)≤ 1.

Calculation of the probability of an event. Example

Let's take Spanish. No. 1 with balls, which was described earlier: 3 blue balls with the numbers 1/3/5 and 3 red balls with the numbers 2/4/6.

Based on this test, several different problems can be considered:

• A - red ball falling out. There are 3 red balls, and there are 6 options in total. This is the simplest example in which the probability of an event is P(A)=3/6=0.5.
• B - rolling an even number. There are 3 even numbers (2,4,6), and the total number of possible numerical options is 6. The probability of this event is P(B)=3/6=0.5.
• C - the occurrence of a number greater than 2. There are 4 such options (3,4,5,6) out of a total number of possible outcomes of 6. The probability of event C is equal to P(C)=4/6=0.67.

As can be seen from the calculations, event C has a higher probability, since the number of probable positive outcomes is higher than in A and B.

Incompatible events

Such events cannot appear simultaneously in the same experience. As in Spanish No. 1 it is impossible to get a blue and a red ball at the same time. That is, you can get either a blue or a red ball. In the same way, an even and an odd number cannot appear in a dice at the same time.

The probability of two events is considered as the probability of their sum or product. The sum of such events A+B is considered to be an event that consists of the occurrence of event A or B, and the product of them AB is the occurrence of both. For example, the appearance of two sixes at once on the faces of two dice in one throw.

The sum of several events is an event that presupposes the occurrence of at least one of them. The production of several events is the joint occurrence of them all.

In probability theory, as a rule, the use of the conjunction “and” denotes a sum, and the conjunction “or” - multiplication. Formulas with examples will help you understand the logic of addition and multiplication in probability theory.

Probability of the sum of incompatible events

If the probability of incompatible events is considered, then the probability of the sum of events is equal to the addition of their probabilities:

P(A+B)=P(A)+P(B)

For example: let's calculate the probability that in Spanish. No. 1 with blue and red balls, a number between 1 and 4 will appear. We will calculate not in one action, but by the sum of the probabilities of the elementary components. So, in such an experiment there are only 6 balls or 6 of all possible outcomes. The numbers that satisfy the condition are 2 and 3. The probability of getting the number 2 is 1/6, the probability of getting the number 3 is also 1/6. The probability of getting a number between 1 and 4 is:

The probability of the sum of incompatible events of a complete group is 1.

So, if in an experiment with a cube we add up the probabilities of all numbers appearing, the result will be one.

This is also true for opposite events, for example in the experiment with a coin, where one side is the event A, and the other is the opposite event Ā, as is known,

P(A) + P(Ā) = 1

Probability of incompatible events occurring

Probability multiplication is used when considering the occurrence of two or more incompatible events in one observation. The probability that events A and B will appear in it simultaneously is equal to the product of their probabilities, or:

P(A*B)=P(A)*P(B)

For example, the probability that in Spanish No. 1, as a result of two attempts, a blue ball will appear twice, equal to

That is, the probability of an event occurring when, as a result of two attempts to extract balls, only blue balls are extracted is 25%. It is very easy to do practical experiments on this problem and see if this is actually the case.

Joint events

Events are considered joint when the occurrence of one of them can coincide with the occurrence of another. Despite the fact that they are joint, the probability of independent events is considered. For example, throwing two dice can give a result when the number 6 appears on both of them. Although the events coincided and appeared at the same time, they are independent of each other - only one six could fall out, the second die has no influence on it.

The probability of joint events is considered as the probability of their sum.

Probability of the sum of joint events. Example

The probability of the sum of events A and B, which are joint in relation to each other, is equal to the sum of the probabilities of the event minus the probability of their occurrence (that is, their joint occurrence):

R joint (A+B)=P(A)+P(B)- P(AB)

Let's assume that the probability of hitting the target with one shot is 0.4. Then event A is hitting the target in the first attempt, B - in the second. These events are joint, since it is possible that you can hit the target with both the first and second shots. But events are not dependent. What is the probability of the event of hitting the target with two shots (at least with one)? According to the formula:

0,4+0,4-0,4*0,4=0,64

The answer to the question is: “The probability of hitting the target with two shots is 64%.”

This formula for the probability of an event can also be applied to incompatible events, where the probability of the joint occurrence of an event P(AB) = 0. This means that the probability of the sum of incompatible events can be considered a special case of the proposed formula.

Geometry of probability for clarity

Interestingly, the probability of the sum of joint events can be represented as two areas A and B, which intersect with each other. As can be seen from the picture, the area of ​​their union is equal to the total area minus the area of ​​their intersection. This geometric explanation makes the seemingly illogical formula more understandable. Note that geometric solutions are not uncommon in probability theory.

Determining the probability of the sum of many (more than two) joint events is quite cumbersome. To calculate it, you need to use the formulas that are provided for these cases.

Dependent Events

Events are called dependent if the occurrence of one (A) of them affects the probability of the occurrence of another (B). Moreover, the influence of both the occurrence of event A and its non-occurrence is taken into account. Although events are called dependent by definition, only one of them is dependent (B). Ordinary probability was denoted as P(B) or the probability of independent events. In the case of dependent events, a new concept is introduced - conditional probability P A (B), which is the probability of a dependent event B, subject to the occurrence of event A (hypothesis), on which it depends.

But event A is also random, so it also has a probability that needs and can be taken into account in the calculations performed. The following example will show how to work with dependent events and a hypothesis.

An example of calculating the probability of dependent events

A good example for calculating dependent events would be a standard deck of cards.

Using a deck of 36 cards as an example, let’s look at dependent events. We need to determine the probability that the second card drawn from the deck will be of diamonds if the first card drawn is:

1. Bubnovaya.
2. A different color.

Obviously, the probability of the second event B depends on the first A. So, if the first option is true, that there is 1 card (35) and 1 diamond (8) less in the deck, the probability of event B:

R A (B) =8/35=0.23

If the second option is true, then the deck has 35 cards, and the full number of diamonds (9) is still retained, then the probability of the following event B:

R A (B) =9/35=0.26.

It can be seen that if event A is conditioned on the fact that the first card is a diamond, then the probability of event B decreases, and vice versa.

Multiplying dependent events

Guided by the previous chapter, we accept the first event (A) as a fact, but in essence, it is of a random nature. The probability of this event, namely drawing a diamond from a deck of cards, is equal to:

P(A) = 9/36=1/4

Since the theory does not exist on its own, but is intended to serve for practical purposes, it is fair to note that what is most often needed is the probability of producing dependent events.

According to the theorem on the product of probabilities of dependent events, the probability of occurrence of jointly dependent events A and B is equal to the probability of one event A, multiplied by the conditional probability of event B (dependent on A):

P(AB) = P(A) *P A(B)

Then, in the deck example, the probability of drawing two cards with the suit of diamonds is:

9/36*8/35=0.0571, or 5.7%

And the probability of extracting not diamonds first, and then diamonds, is equal to:

27/36*9/35=0.19, or 19%

It can be seen that the probability of event B occurring is greater provided that the first card drawn is of a suit other than diamonds. This result is quite logical and understandable.

Total probability of an event

When a problem with conditional probabilities becomes multifaceted, it cannot be calculated using conventional methods. When there are more than two hypotheses, namely A1, A2,…, A n, ..forms a complete group of events provided:

• P(A i)>0, i=1,2,…
• A i ∩ A j =Ø,i≠j.
• Σ k A k =Ω.

So, the formula for the total probability for event B with a complete group of random events A1, A2,..., A n is equal to:

A look into the future

The probability of a random event is extremely necessary in many areas of science: econometrics, statistics, physics, etc. Since some processes cannot be described deterministically, since they themselves are probabilistic in nature, special working methods are required. The theory of event probability can be used in any technological field as a way to determine the possibility of an error or malfunction.

We can say that by recognizing probability, we in some way take a theoretical step into the future, looking at it through the prism of formulas.

1. Formulas for calculating the probability of events

1.3.1. Sequence of independent tests (Bernoulli circuit)

Suppose that some experiment can be carried out repeatedly under the same conditions. Let this experience be made n times, i.e., a sequence of n tests.

Definition. Subsequence n tests are called mutually independent , if any event related to a given test is independent of any events related to other tests.

Let's assume that some event A likely to happen p as a result of one test or not likely to happen q= 1- p.

Definition . Sequence of n tests forms a Bernoulli scheme if the following conditions are met:

subsequence n tests are mutually independent,

2) probability of an event A does not change from trial to trial and does not depend on the result in other trials.

Event A is called the “success” of the test, and the opposite event is called “failure.” Consider the event

=( in n tests happened exactly m“success”).

To calculate the probability of this event, the Bernoulli formula is valid

p() =
, m = 1, 2, …, n , (1.6)

Where - number of combinations of n elements by m :

=
=
.

Example 1.16. The die is tossed three times. Find:

a) the probability that 6 points will appear twice;

b) the probability that the number of sixes will not appear more than twice.

Solution . We will consider the “success” of the test to be when the side with the image of 6 points appears on the die.

a) Total number of tests – n=3, number of “successes” – m = 2. Probability of “success” - p=, and the probability of “failure” is q= 1 - =. Then, according to Bernoulli's formula, the probability that, as a result of throwing a die three times, the side with six points will appear twice, will be equal to

.

b) Let us denote by A an event that means that a side with a score of 6 will appear no more than twice. Then the event can be represented as the sum of three incompatible events A=
,

Where IN 3 0 – an event when the edge of interest never appears,

IN 3 1 - event when the edge of interest appears once,

IN 3 2 - event when the edge of interest appears twice.

Using the Bernoulli formula (1.6) we find

p(A) = p (
) = p(
)=
+
+
=

=
.

1.3.2. Conditional probability of an event

Conditional probability reflects the influence of one event on the probability of another. Changing the conditions under which the experiment is carried out also affects

on the probability of occurrence of the event of interest.

Definition. Let A And B– some events, and probability p(B)> 0.

Conditional probability events A provided that the “event Balready happened” is the ratio of the probability of the occurrence of these events to the probability of an event that occurred earlier than the event whose probability is required to be found. Conditional probability is denoted as p(A B). Then by definition

p (A  B) =
. (1.7)

Example 1.17. Two dice are tossed. The space of elementary events consists of ordered pairs of numbers

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).

In Example 1.16 it was determined that the event A=(number of points on the first die > 4) and event C=(sum of points is 8) dependent. Let's make a relation

.

This relationship can be interpreted as follows. Let us assume that the result of the first throw is known to be that the number of points on the first die is > 4. It follows that throwing the second die can lead to one of the 12 outcomes that make up the event A:

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .

At this event C only two of them can match (5,3) (6,2). In this case, the probability of the event C will be equal
. Thus, information about the occurrence of an event A influenced the likelihood of an event C.

Probability of events happening

Multiplication theorem

Probability of events happeningA 1 A 2  A n is determined by the formula

p(A 1 A 2  A n)= p(A 1)p(A 2  A 1)) p(A n  A 1 A 2  A n- 1). (1.8)

For the product of two events it follows that

p(AB)= p(A B)p{B)= p(B A)p{A). (1.9)

Example 1.18. In a batch of 25 products, 5 products are defective. 3 items are selected at random in succession. Determine the probability that all selected products are defective.

Solution. Let's denote the events:

A 1 = (first product is defective),

A 2 = (second product is defective),

A 3 = (third product is defective),

A = (all products are defective).

Event A is the product of three events A = A 1 A 2 A 3 .

From the multiplication theorem (1.6) we get

p(A)= p( A 1 A 2 A 3 ) = p(A 1) p(A 2  A 1))p(A 3  A 1 A 2).

The classical definition of probability allows us to find p(A 1) is the ratio of the number of defective products to the total number of products:

p(A 1)= ;

p(A 2) – This the ratio of the number of defective products remaining after the removal of one to the total number of remaining products:

p(A 2  A 1))= ;

p(A 3) – this is the ratio of the number of defective products remaining after the removal of two defective ones to the total number of remaining products:

p(A 3  A 1 A 2)=.

Then the probability of the event A will be equal

p(A) ==
.

So, let's talk about a topic that interests a lot of people. In this article I will answer the question of how to calculate the probability of an event. I will give formulas for such a calculation and several examples to make it clearer how this is done.

What is probability

Let's start with the fact that the probability that this or that event will occur is a certain amount of confidence in the eventual occurrence of some result. For this calculation, a total probability formula has been developed that allows you to determine whether the event you are interested in will occur or not, through the so-called conditional probabilities. This formula looks like this: P = n/m, the letters can change, but this does not affect the essence itself.

Examples of probability

Using a simple example, let's analyze this formula and apply it. Let's say you have a certain event (P), let it be a throw of a dice, that is, an equilateral die. And we need to calculate what is the probability of getting 2 points on it. To do this, you need the number of positive events (n), in our case - the loss of 2 points, for the total number of events (m). A roll of 2 points can only happen in one case, if there are 2 points on the dice, since otherwise the sum will be greater, it follows that n = 1. Next, we count the number of rolls of any other numbers on the dice, per 1 dice - these are 1, 2, 3, 4, 5 and 6, therefore, there are 6 favorable cases, that is, m = 6. Now, using the formula, we make a simple calculation P = 1/6 and we find that the roll of 2 points on the dice is 1/6, that is, the probability of the event is very low.

Let's also look at an example using colored balls that are in a box: 50 white, 40 black and 30 green. You need to determine what is the probability of drawing a green ball. And so, since there are 30 balls of this color, that is, there can only be 30 positive events (n = 30), the number of all events is 120, m = 120 (based on the total number of all balls), using the formula we calculate that the probability of drawing a green ball is will be equal to P = 30/120 = 0.25, that is, 25% of 100. In the same way, you can calculate the probability of drawing a ball of a different color (black it will be 33%, white 42%).

Want to know the mathematical odds of your bet being successful? Then there is two good news for you. First: to calculate cross-country ability, you don’t need to carry out complex calculations and spend a lot of time. It is enough to use simple formulas, which will take a couple of minutes to work with. Second: after reading this article, you can easily calculate the probability of any of your transactions passing.

To correctly determine cross-country ability, you need to take three steps:

• Calculate the percentage of probability of the outcome of an event according to the bookmaker’s office;
• Calculate the probability using statistical data yourself;
• Find out the value of the bet, taking into account both probabilities.

Let's look at each of the steps in detail, using not only formulas, but also examples.

The first step is to find out with what probability the bookmaker himself estimates the chances of a particular outcome. It’s clear that bookmakers don’t set odds just like that. To do this we use the following formula:

PB=(1/K)*100%,

where P B is the probability of the outcome according to the bookmaker’s office;

K – bookmaker odds for the outcome.

Let’s say that the odds for London Arsenal’s victory in the match against Bayern Munich are 4. This means that the probability of their victory is assessed by the bookmaker as (1/4)*100%=25%. Or Djokovic plays against Youzhny. The multiplier for Novak's victory is 1.2, his chances are (1/1.2)*100%=83%.

This is how the bookmaker itself evaluates the chances of success of each player and team. Having completed the first step, we move on to the second.

Calculation of the probability of an event by the player

The second point of our plan is our own assessment of the probability of the event. Since we cannot mathematically take into account such parameters as motivation and game tone, we will use a simplified model and use only statistics from previous meetings. To calculate the statistical probability of an outcome, we use the formula:

PAND=(UM/M)*100%,

WherePAND– probability of an event according to the player;

UM – the number of successful matches in which such an event occurred;

M – total number of matches.

To make it clearer, let's give examples. Andy Murray and Rafael Nadal played 14 matches between themselves. In 6 of them the total was less than 21 in games, in 8 the total was more. You need to find out the probability that the next match will be played with a higher total: (8/14)*100=57%. Valencia played 74 matches against Atlético at Mestalla, in which they won 29 victories. Probability of Valencia winning: (29/74)*100%=39%.

And we learn all this only thanks to the statistics of previous games! Naturally, it will not be possible to calculate such a probability for a new team or player, so this betting strategy is only suitable for matches in which the opponents meet more than once. Now we know how to determine the bookmaker's and our own probabilities of outcomes, and we have all the knowledge to move on to the last step.

Determining the value of a bet

The value (value) of a bet and the passability have a direct connection: the higher the value, the higher the chance of passing. The value is calculated as follows:

V=PAND*K-100%,

where V is value;

P I – probability of outcome according to the bettor;

K – bookmaker odds for the outcome.

Let’s say we want to bet on Milan’s victory in the match against Roma and we calculate that the probability of the “red-blacks” winning is 45%. The bookmaker offers us odds of 2.5 for this outcome. Would such a bet be valuable? We carry out calculations: V=45%*2.5-100%=12.5%. Great, we have a valuable bet with good chances of passing.

Let's take another case. Maria Sharapova plays against Petra Kvitova. We want to make a deal for Maria to win, the probability of which, according to our calculations, is 60%. Bookmakers offer a 1.5 multiplier for this outcome. We determine the value: V=60%*1.5-100=-10%. As you can see, this bet is of no value and should be avoided.

Probability of bet passing: conclusion

When calculating the bet's passability, we used a simple model, which is based only on statistics. When calculating the probability, it is advisable to take into account many different factors that are individual in each sport. It happens that it is non-statistical factors that have more influence. Without this, everything would be simple and predictable. Once you choose your niche, you will eventually learn to take all these nuances into account and make a more accurate assessment of your own likelihood of events, including many other influences. The main thing is to love what you do, gradually move forward and improve your skills step by step. Good luck to you and success in the exciting world of betting!

There will also be problems for you to solve on your own, to which you can see the answers.

General statement of the problem: the probabilities of some events are known, and you need to calculate the probabilities of other events that are associated with these events. In these problems, there is a need for operations with probabilities such as addition and multiplication of probabilities.

For example, while hunting, two shots are fired. Event A- hitting a duck with the first shot, event B- hit from the second shot. Then the sum of events A And B- hit with the first or second shot or with two shots.

Problems of a different type. Several events are given, for example, a coin is tossed three times. You need to find the probability that either the coat of arms will appear all three times, or that the coat of arms will appear at least once. This is a probability multiplication problem.

Addition of probabilities of incompatible events

Addition of probabilities is used when you need to calculate the probability of a combination or logical sum of random events.

Sum of events A And B denote A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B– an event that occurs if and only if the event occurred during observation A or event B, or simultaneously A And B.

If events A And B are mutually inconsistent and their probabilities are given, then the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.

Probability addition theorem. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:

For example, while hunting, two shots are fired. Event A– hitting a duck with the first shot, event IN– hit from the second shot, event ( A+ IN) – a hit from the first or second shot or from two shots. So, if two events A And IN– incompatible events, then A+ IN– the occurrence of at least one of these events or two events.

Example 1. There are 30 balls of the same size in a box: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball will be picked up without looking.

Solution. Let us assume that the event A- “the red ball is taken”, and the event IN- “The blue ball was taken.” Then the event is “a colored (not white) ball is taken.” Let's find the probability of the event A:

and events IN:

Events A And IN– mutually incompatible, since if one ball is taken, then it is impossible to take balls of different colors. Therefore, we use the addition of probabilities:

The theorem for adding probabilities for several incompatible events. If events constitute a complete set of events, then the sum of their probabilities is equal to 1:

The sum of the probabilities of opposite events is also equal to 1:

Opposite events form a complete set of events, and the probability of a complete set of events is 1.

Probabilities of opposite events are usually indicated in small letters p And q. In particular,

from which the following formulas for the probability of opposite events follow:

Example 2. The target in the shooting range is divided into 3 zones. The probability that a certain shooter will shoot at the target in the first zone is 0.15, in the second zone – 0.23, in the third zone – 0.17. Find the probability that the shooter will hit the target and the probability that the shooter will miss the target.

Solution: Find the probability that the shooter will hit the target:

Let's find the probability that the shooter will miss the target:

More complex problems, in which you need to use both addition and multiplication of probabilities, can be found on the page "Various problems involving addition and multiplication of probabilities".

Addition of probabilities of mutually simultaneous events

Two random events are called joint if the occurrence of one event does not exclude the occurrence of a second event in the same observation. For example, when throwing a die the event A The number 4 is considered to be rolled out, and the event IN– rolling an even number. Since 4 is an even number, the two events are compatible. In practice, there are problems of calculating the probabilities of the occurrence of one of the mutually simultaneous events.

Probability addition theorem for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events has the following form:

Since events A And IN compatible, event A+ IN occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:

Event A will occur if one of two incompatible events occurs: or AB. However, the probability of the occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:

Likewise:

Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:

When using formula (8), it should be taken into account that events A And IN can be:

• mutually independent;
• mutually dependent.

Probability formula for mutually independent events:

Probability formula for mutually dependent events:

If events A And IN are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is:

Example 3. In auto racing, when you drive the first car, you have a better chance of winning, and when you drive the second car. Find:

• the probability that both cars will win;
• the probability that at least one car will win;

1) The probability that the first car will win does not depend on the result of the second car, so the events A(the first car wins) and IN(the second car will win) – independent events. Let's find the probability that both cars win:

2) Find the probability that one of the two cars will win:

More complex problems, in which you need to use both addition and multiplication of probabilities, can be found on the page "Various problems involving addition and multiplication of probabilities".

Solve the addition of probabilities problem yourself, and then look at the solution

Example 4. Two coins are tossed. Event A- loss of the coat of arms on the first coin. Event B- loss of the coat of arms on the second coin. Find the probability of an event C = A + B .

Multiplying Probabilities

Probability multiplication is used when the probability of a logical product of events must be calculated.

In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.

Probability multiplication theorem for independent events. Probability of simultaneous occurrence of two independent events A And IN is equal to the product of the probabilities of these events and is calculated by the formula:

Example 5. The coin is tossed three times in a row. Find the probability that the coat of arms will appear all three times.

Solution. The probability that the coat of arms will appear on the first toss of a coin, the second time, and the third time. Let's find the probability that the coat of arms will appear all three times:

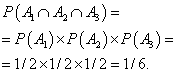
Solve probability multiplication problems on your own and then look at the solution

Example 6. There is a box of nine new tennis balls. To play, three balls are taken, and after the game they are put back. When choosing balls, played balls are not distinguished from unplayed balls. What is the probability that after three games there will be no unplayed balls left in the box?

Example 7. 32 letters of the Russian alphabet are written on cut-out alphabet cards. Five cards are drawn at random one after another and placed on the table in order of appearance. Find the probability that the letters will form the word "end".

Example 8. From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards will be of different suits.

Example 9. The same task as in example 8, but each card after being removed is returned to the deck.

More complex problems, in which you need to use both addition and multiplication of probabilities, as well as calculate the product of several events, can be found on the page "Various problems involving addition and multiplication of probabilities".

The probability that at least one of the mutually independent events will occur can be calculated by subtracting from 1 the product of the probabilities of opposite events, that is, using the formula.