The paradox of the lottery and Bernoulli's law of large numbers. The paradox of lotteries, or programs for selecting numbers Analyzer of numbers in the lottery

Analysis of lotto (numerical lotteries) is carried out based on the results of past draws.

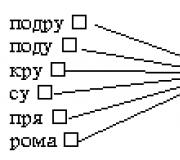
Each number lotto player uses his own analysis system. Previously, this was done in school notebooks in a box, carefully recording each past lottery draw on a separate line. Nowadays the EXSEL program from the Microsoft Office package is very convenient. In it you can create the required number of sheets, enter formulas for calculating various combinations, and highlight the required cells with color. Here is an example of use:

I have developed my own numerical lottery analysis system and use its results to select numbers. This system was translated into program code and now anyone can use it.

I would be very grateful for your advice and recommendations. Please send them from the Feedback page of the site. If they are worthy, changes will be made to the published online lotto analysis system.

Below are the lotteries for which this analysis can be applied (their list will be expanded as development progresses):

For more diligent players (you need to enter more numbers) there is: lotto analysis for twenty draws

Explanations for the numerical lottery analysis table

First table:

Circulation- the last ten draws of the numerical lottery (lotto) are used for analysis. Don’t be too alarmed by the fact that you need to enter the numbers of ten draws. This is done once. In the future, you need to record the numbers of only one last circulation.

Drawn numbers (balls)- numbers in the pivot table are displayed in ascending order.

Sum- sum of circulation numbers

Even- even numbers of balls of the drawn draw, their number is indicated in brackets.

Not even- non-even numbers of balls in the drawn draw, their number is indicated in brackets

Distance between balls- the difference between adjacent (ascending) numbers of balls (between the first and second, second and third, third and fourth, fourth and fifth).

The averages are shown at the bottom of each column.

Second table:

Replays- the numbers of the balls of the last drawing, which coincide with the numbers of the previous one and after a certain number of drawings, their number is indicated in brackets. This information shows the draws (where there are no matches - the value is zero), the numbers of which may appear in the next draw.

Third table:

Almost every number lottery player compiles such a table. In it horizontally: numbers, vertically: circulations. The dropped balls fit into the intersections. The number of occurrences of a particular number vertically in a line is summed up below "for 10".

Parameter "N"<" - a number that determines the probable numbers of the next draw. The larger it is, the greater the probability of the ball falling out. The determination of this number is based on two provisions:

the most probable number of successes in J. Bernoulli's scheme;

According to the works of the Russian mathematician A. A. Markov, a random variable “remembers” its last occurrence and “does not remember” the penultimate occurrence, as well as those occurrences that were before, before, before... last.

You can use this parameter like this: Select numbers that have not been drawn during ten draws and numbers that have an indicator greater than “zero” numbers. But keep in mind that the lottery is not the most predictable game - in almost every draw, balls with a lower value are drawn. And a controversial question about the numbers of the last circulation. In "N"<" показатели этих номеров всегда выше "нулевых". И на практике получается, что в каждом третьем тираже есть совпадения с номерами предыдущего тиража. Какой из выпавших шаров повторится в следующем тираже расчитать проблематично. Поэтому учитывайте номера последного тиража как прогнозируемые.

The very last line of the third table is empty. You print out the table and use this line to select numbers.

After clicking the " Lottery analysis"You will be presented with an analysis of the lottery. Save the resulting page on your computer and you will have the opportunity to add the results of subsequent draws.

In connection with the entry into force yesterday, June 30, 2009, of paragraph 1 of article 17, paragraph 1 of article 18 and article 19
FEDERAL LAW of December 29, 2006 N 244-FZ “ON STATE REGULATION OF ACTIVITIES IN ORGANIZING AND CONDUCTING GAMBLING AND ON AMENDMENTS TO SOME LEGISLATIVE ACTS OF THE RUSSIAN FEDERATION” (adopted by the State Duma of the Federal Assembly of the Russian Federation 12/20/2006), http://nalog.consultant. ru/doc64924.html

THE PARADOX OF THE LOTTERY AND BERNOULLI'S LAW OF LARGE NUMBERS

Opportunity - an opportunity to be disappointed

(“Aphorisms, quotes, and catchwords”,
http://aphorism-list.com/t.php?page=vozmojnost)

Your chances of winning the lottery will increase
if you buy a ticket

Winston Groom (from Forrest Gump Rules)
(“Aphorisms about games”,
http://letter.com.ua/aphorism/game1.php)

"The Lottery Paradox"

It is quite expected (and philosophically verifiable [English]) that this particular ticket will not win, but one cannot expect that no ticket will win” (“Academics”, List of Paradoxes, http://dic.academic.ru/dic.nsf /ruwiki/165304).

“The paradox of the lottery (such as sports lotto)

Most lottery players (in which the winnings are distributed among all the winners, as in sports lotto) usually do not bet on “too symmetrical” combinations, although all combinations are equally possible. The reason is simple. Players know from experience that, as a rule, non-symmetrical combinations win. In fact, it is more profitable to bet on the most symmetrical combinations precisely because... Why?" (excerpts from the book: G. Szekely. Paradoxes in probability theory and mathematical statistics. M.: Mir. - 1990, http://arbuz.uz/t_paradox.html).

SOLUTION

Everyone has played some kind of game in their life, not necessarily gambling, which is, in one way or another, related to probability. And if someone didn’t play, they probably tossed a coin a couple of times in their life. Just like that, for fun or when solving some issue on which it turned out to be overwhelming or impossible to make a choice on one’s own. And I did the same thing as a child. But even then, some doubt crept into my head about the correctness of justifying my choice of solutions to even trivial issues by tossing a coin. Apparently, even then I didn’t want to entrust my own right of choice to blind chance. But not so much because I myself can choose the best option right now and for myself, but more because such a choice will not be fair. So fair that without any further thought or internal hesitation I could accept it and act in accordance with this choice. And then I completely stopped further attempts at making decisions in such a simple way when my fears were confirmed while watching one of the popular Indian films that took place here in the 80s. If I'm not mistaken, it was the film "Revenge and Law." In it, one of the main characters, making a choice of something, tossed a coin with a serious look. And everything would have been fine, but only when he was shot after all, and he gave his “lucky coin”, it turned out that it had two identical sides. Apparently, this hero has well learned the first rule of success: if you want to win at a casino, become its owner.

To the question of the problem given by Székely in his book about why it is MORE PROFITABLE to choose symmetrical options for the geometric arrangement of numbers on the card field, the answer is not so complicated. The conclusion follows based on three conditions:

1) all options: both symmetrical and asymmetrical are equally probable;

2) most players choose asymmetrical options;

3) the amount of winnings received depends on the number of: a) participants, b) winners (according to winning categories, of course);

Therefore, from the point of view of benefit, that is, an increase in the possible profit when guessing, symmetric options will be guessed by a much smaller number of players with the same number of participants in the lottery, and the winning amount will be divided among a much smaller number of winners.

But on the other hand, if everything were that simple, then there would be no difficulties in determining the probability of certain events. And there are no fewer paradoxes and various paradoxical problems in probability theory, or even much more, than in other branches of science (in the same mathematics, logic, physics). For example, this task.

"The Dice Paradox"

A fair die, when thrown, has an equal chance of landing on any of the sides 1,2,3,4,5 or 6. (The sum of the points on opposite sides is 7, i.e. falling on 1 means rolling a 6, etc.) .

In the case of throwing 2 dice, the sum of the numbers drawn is between 2 and 12. Both 9 and 10 can be obtained in two different ways: 9 = 3 + 6 = 4 + 5 and 10 = 4 + 6 = 5 + 5. In the problem with three dice, 9 and 10 are obtained in six ways. Why then does 9 appear more often when two dice are thrown, and 10 when three are thrown? (excerpts from the book: G. Szekely. Paradoxes in probability theory and mathematical statistics. M.: Mir. - 1990, http://arbuz.uz/t_paradox.html)."

There is no paradox in this problem. The paradox, or rather the trick, is hidden in incomplete information: the number of possible combinations is greater than indicated. Because only the types of options are indicated, the methods of composition that need to be distributed over the number of bones.

The answer is simple: 9 appears more often when two dice are rolled, and 10 when three dice are rolled, because the probability of rolling a total of 9 with two dice is greater than the probability of rolling a total of 10 with three dice, which reflects the ratio of the number of options compilation of these amounts.

Number of options for summing up:

A. 9 on two dice: 3+6 (2 possible options, that is, on the first 3 on the second 6 and vice versa) and 4+5 (2 options). Total: 4 options

10 on two dice: 4+6 (2 var.) and 5+5 (1 var.). Total: 3 options

The odds ratio is in favor of the sum 9.

B. 9 on three dice: 1+2+6 (6 varieties), 1+3+5 (6 varieties), 1+4+4 (3 varieties), 2+2+5 (3 varieties) , 2+3+4 (6 var.), 3+3+3 (1 var.). Total: 25 options

10 on three dice: 1+3+6 (6 options), 1+4+5 (6 options), 2+2+6 (3 options), 2+3+5 (6 options), 2 +4+4 (3 options), 3+3+4 (3 options), 4+4+2 (3 options) Total: 30 options

The odds ratio is in favor of the sum 10.

Why does the probability of events give rise to so many contradictions?

I may be wrong, but in my opinion, even mathematicians, not to mention those who are not at all familiar with the theory of probability, are captive of one false initial premise about the probability distribution. This is the idea that events occur only according to their probability, without taking into account the distribution of probability over time. Life does not always go according to calculated patterns and exactly as it is described mathematically. A reflection of this two-facedness: mathematical calculation and at the same time not a coincidence with it, is given in the following paradox.

THE PARADOX OF BERNOULLI'S LAW OF LARGE NUMBERS

“The ratio of heads or tails to the total number of attempts with a large number of throws tends to 1/2. Some players believe that with a series of heads, the probability of landing tails increases. And at the same time, the coins have no memory, they do not know the previous throws, and each time the probability of heads or tails falling out is 1/2. Even if before that 1000 coats of arms fell in a row. Doesn’t this contradict Bernoulli’s law?” (excerpts from the book: G. Szekely. Paradoxes in probability theory and mathematical statistics. M.: Mir. - 1990, http://arbuz.uz/t_paradox.html).

Bernoulli's law of large numbers

“Let a sequence of independent trials be carried out, as a result of each of which event A may or may not occur, and the probability of the occurrence of this event is the same for each trial and is equal to p. If event A actually occurred m times in n trials, then the ratio m/n is called, as we know, the frequency of occurrence of event A. Frequency is a random variable, and the probability that the frequency takes the value m/n is expressed by Bernoulli’s formula ...

The law of large numbers in Bernoulli's form is as follows: with a probability arbitrarily close to unity, it can be argued that with a sufficiently large number of experiments, the frequency of occurrence of event A differs as little as desired from its probability, i.e....

...in other words, with an unlimited increase in the number n of experiments, the frequency m/n of event A converges in probability to P(A)" (Theory of Probability, §5. 3. Bernoulli's Law of Large Numbers. , http://www.toehelp.ru/ theory/ter_ver/5_3)

Thus, from the contradictions contained in these paradoxes, a general problem can be formulated.

Controversies:

1. The paradox of the lottery - the probability of winning a specific ticket is negligible, but the probability of winning any ticket is 1, that is, 100 percent;

2. The paradox of Bernoulli's law of large numbers - the probability of getting any option is equivalent, but in reality it should change as some options get out more to bring the probability to balance.

The problem, in my opinion, lies in the misunderstanding of the uneven distribution of probability over the number of options or, in other words, the dependence of the probability of one option of an event on another in a time context.

No one will argue that the sum of the probabilities of the event options is equal to one. But why does everyone think that the distribution among options is even? This approach completely ignores the variability of the world over time. And the same coin sides should then strictly alternate in turn: heads, tails, heads, tails. Then the probability distribution calculated by the formula will completely coincide with the actual one FOR ANY SPECIFIC TIME PERIOD. Because within this time period, the number of different options dropped will be the same. But in reality this is not the case. Within individual periods, the probability of each event option varies from 0 to 1 (from zero to one hundred percent). For example, when out of ten times, heads come up all ten times (or red, if it’s roulette in a casino). I know of a case where the roulette wheel came up black 15 times in a row. From the point of view of calculating probability, this is generally impossible if we take it as a unit, that is, the sum of all possible options, for example, 20 occurrences, which include these fifteen. And this, by the way, continuing the thought, for some reason did not lead to the next fifteen drops of red. Players call such hits in a row as streaks. Series are observed in sports, and everywhere in general.

Would you say that Bernoulli's law describes periods with large, "unlimited numbers of experiences" and within these limits it is true? Then why shouldn’t the same coin fall out first 1000 times on one side in a row, and then a thousand times on the other? After all, the law in this case is not violated one bit? In reality this does not happen. In fact, any long series of occurrences of two possible variants of events (A and B, which can be replaced, for example, by “heads” and “tails”) will closely correspond to the pattern of occurrences:

A, B, A, B, AAA, B, AA, BB, AA, BBBBBBB, AA, BBB, A, BBBBBBB, AAA, B, AA, BB, A, B, AAAA, B, AA, BBB, AAAA, B, A, B, A... (30 A and B each, 60 in total).

As you can see, within each specific segment (fallout periods or time periods) there are unevennesses. And the duration of the “series” of occurrences of one option a) in a row and b) within a period (for example, 10 occurrences) may fluctuate. Theoretically, the amplitude of such oscillations is not limited by anything, but there are no practically unlimited duration series. That is, there is a certain limit to which the duration of the “series,” its “length,” increases. These two restrictions regulate the balance of the probability of event options: firstly, the variability of options within an arbitrary period (time), in other words, the change in the “length” of series from 1 to several repetitions in a row, and secondly, the limitation of the length and frequency of series in within an arbitrary period (time). This achieves a variety of events, variability.

This probability distribution is noted by players who choose asymmetrical options for the arrangement of numbers on a lottery card. They do not proceed from an equal probability distribution for the number of numbers, that is, their equally possible occurrence, but precisely from an uneven probability distribution over the numbers. For some reason, the same numbers have not yet appeared, not only in two draws in a row, but in the mass of all draws. I can say this with confidence based on studying the “Sportloto 5 out of 36” lottery, which has been running for decades. In two draws in a row, a maximum of 1 number from the previous draw will appear (quite often - about a quarter of the draws), 2 (in isolated cases), 3 (in more rare cases). According to the theory of probability, someday all five numbers would come out the same for two draws in a row. But this would take thousands of years, even if the circulations were held every day instead of once a week. This follows if we assume that the total number of possible options in the “Sportloto 5 out of 36” lottery (36 * 35 * 34 * 33 * 32 / 1 * 2 * 3 * 4 * 5) = 376.992, and repeat five numbers of the previous draw will occur no earlier than all possible options have been drawn at least once, which will happen when conducting 1 draw per day, taking into account leap years for: 376.992 / (365 * 4 + 1) * 4 = 1032.1478 ~ 1032 of the year. But even after a complete search of all possible options in a row, two identical editions may not appear for several thousand years, and perhaps never.

Therefore, I absolutely agree with players choosing the most frequently dropped, asymmetrical options. Because waiting for the option to appear, for example, from the film “Sportloto - 82” with M. Pugovkin and M. Kokshenov - 1,2,3,4,5,6 is simply unrealistic. You might as well wait for rain on Mars.
I will add that, having fixed the probability distribution in a certain way, I saw that the types of options similar to those given from the film make up an insignificant fraction of a percent of all other types, classes of options that appear, and according to the theory of probability they are equally possible.

The paradox of the lottery arises due to the fact that the probability of winning each specific ticket separately, that is, any one, is negligible, tending to zero, but the probability of winning any one specific ticket is one hundred percent. Because the probability of specific numbers appearing in a specific draw is distributed unequally among all options. Roughly speaking, one hundred percent of the probability is divided not into the entire mass of tickets, but into two parts - all the winners (that is, one, for simplicity) and all the losers (all the rest). Thus, everyone and no one has a chance to win. Because it is impossible to know WHICH ticket will win, but we know in advance that SOME ONE ticket will win (without going into details of the number of winners and winning conditions).
At this point, no matter how funny it may seem, the correctness of “female logic” becomes obvious, which claims that the probability of a meteorite falling on Red Square is not one in several million, but fifty to fifty - either it will fall or not.
Apparently, such a famous mathematician as Poincare also held a similar opinion to mine. “Poincaré once remarked sarcastically that everyone believes in the universality of the normal distribution: physicists believe because they think that mathematicians have proven its logical necessity, and mathematicians believe because they believe that physicists have verified it with laboratory experiments” (De Moivre's Paradox , excerpts from the book: G. Székely, Paradoxes in probability theory and mathematical statistics (M.: Mir. - 1990, http://arbuz.uz/t_paradox.html).

That is, the lottery paradox arises due to an incorrect initial premise - the probability distribution is not uniform within a particular period, but variable. And if we take one circulation for a separate period, then ALL possible options CANNOT appear in it, but only ONE will appear. Therefore, the contradictory understanding of probability disappears: the probability of the absolute majority of options appearing will be equal to zero, and only the probability of one option will be equal to one.

There are no contradictory conditions in the lottery paradox:

1) only one option appears in a particular draw out of all possible ones (one ticket wins);

2) there are many more possible options.

Consequently, the probability of expecting to win only ONE of all possible options (tickets) tends to one, and the probability of expecting to win ALL REMAINING ONE options (tickets) tends to zero.

There is also no contradiction in Bernoulli's paradox of large numbers:

1) the probability of getting one of the possible options is half – 0.5;

2) the expectation of a change in the probability of the second of the possible options falling out after a series of falling out of the first one changes.

Consequently, the probability of the event as a whole does not change, that is, the sum of the probabilities of the options remains the same, but within a single period, especially if it is incomparably small in relation to the sum of all possible periods of occurrences, the probability changes, which is reflected in the expectations of the players.

Try to prove to the winner of a large sum that the probability of this was infinitesimal. Moreover, try to prove this to several or thousands of such people. The probability of even being born was absolutely negligible for some, but, nevertheless, it happened.
Many compare the impossibility of winning to the possibility of a meteorite falling on one's head or being struck by lightning. Try to prove that this is impossible, because the probability of this is infinitely small, to those affected by them. Like, for example, a woman who was healed from a lightning strike: “A unique case was recorded in the Serbian city of Slivovica, reports the DELFI portal. Lightning hit 51-year-old Nada Akimovich, who previously suffered from arrhythmia. However, as a result of exposure to a powerful discharge of electric current, the disease disappeared” (Lightning strike healed a woman/Dni.ru, 23:23 / 07/10/2009, http://www.dni.ru/incidents/2009/7/10/170321.html ) – or to a boy from Germany: “...The chance of being hit by a meteorite is 1 in a hundred million... “First I saw a large fireball, and then I suddenly felt pain in my hand.” (A German boy was hit by a meteorite / MIGnews.com, 06/14/2009, 02:42,

Thus, THERE IS NO CONTRADOX IN THE LOTTERY PARADOX, JUST IN THE PARADOX OF BERNOULLI'S LARGE NUMBERS.

01.07.2009 03:00 – 6.30

Photo - Gosloto, http://www.gosloto.ru/index.php?id=93

PS: the probability of another article appearing instead of this one was close to 100 percent, today or in the coming days. However, this did not happen. And the appearance of this article in the coming weeks was generally close to zero. However, it happened.

Reviews

"The chance of being hit by a meteorite is 1 in a hundred million... A German boy was hit by a meteorite." The example is not identical to winning the lottery, since it is not at all clear where the ratio “1 to one hundred million” comes from.

If we talk about the lottery, then, let’s say for Israel, winning the first prize is 1 in 18 million. The person who won knows that his chance was negligible, but he sees that people win at least once every month or two, and therefore, even “knowing”, he does not realize the “smallness” of his chance. The catch is that the chance is small only for a specific person, but for the country as a whole, with a population of 6 million, it is very logical to win one of 10-20 games (not everyone plays, but each player can fill out more than one form).
A classic scenario, as in the birthday paradox.

As for the numbers - not for me, I took the quote. And it’s not so important, in theory, that the numbers may not be entirely accurate, the main thing is that they illustrate the idea - even very rare events have happened, are happening and will always happen. Therefore, I think the example is still identical.

Yes, you yourself pleased with the numbers, Dmitry. Speaking about Israel, purely in Jewish terms, they reduced the country’s population a little, maybe by a couple of million :) And then why did you decide that the main prize is won “once or twice a month.” This is out of the blue, sorry. And don’t think that people are all stupid, that they don’t understand the insignificance of chance. They understand! But the costs compared to the profits are negligible, just as the chance of winning is negligible. So there is, one might say, a balance here. And some people actually win all their lives! I recently read about a woman who, after a health misfortune, began playing every quiz and lottery available. So her whole apartment is littered with various prizes. The guy often won the Russian Lotto with 1-2 tickets, when others received nothing even with a pack or two. I myself participated in the lottery at the presentation, where the 1st main prize - a computer - was won by a woman who bought a computer, that is, she had only 1 ticket-receipt. And the second prize - a monitor - was won by the guy who bought the monitor, also with the 1st ticket-check. There were a hundred or two people. However, fraud is also possible here, which is not uncommon in our country.

Well, there is no paradox. For one person, the probability of winning tends to zero, and for a country, it approaches one hundred percent. This is my conclusion. I talked about birthdays, but it is completely inadequate for this, as far as I remember. Suffice it to remember how they recruit for classrooms.

“they reduced the country’s population by a couple of million... why did you decide that the main prize is won “once or twice a month”. This is out of the blue, excuse me...” - about the number is true, due to my mistake I was using data for 2000, but about the “from the ceiling” - you’re wrong. It just so happened that for almost 5 years I worked as the head of the computer department of the Israeli lottery and all statistics went through the database I managed. The number of known users is updated every 10 years (so the data is from 2000), but the winnings and the number of winners with their amounts (even if it is only 10 shekels) are recorded twice a week. So this is not an assumption, but a statement.

“And don’t think that people are all stupid, that they don’t understand the insignificance of the chance” - I didn’t say that. My quote: “even though he “knows,” he does not realize the “smallness” of his chance.” A person is not able to comprehend very large or very small numbers, i.e. It is important for him to walk 10 km or 20 km, but the distance to the moon is 380 thousand or 400 thousand does not matter - he is simply not able to realize this, since he himself does not personally operate with such distances.
The odds can easily be reduced from 18 million to 1 to 9 million to 1 by just buying two tickets. A person imagines this as an incredible advancement. And it’s not about stupidity, but about awareness. In my memory, it’s rare... VERY RARELY that a person buys JUST ONE column in the lotto, precisely for this reason: to increase the chance by two, three,...- 10 times. Although essentially it doesn't matter.

Ahh.. so it’s you Systematism and someone else there, then, sir? ok:) By the way, you didn’t respond to one of my old reviews, and God bless you. I forgot myself.

AS: having read to the words “for almost 5 years I worked as the head of the computer department of the Israeli...”, the reader automatically added “intelligence” and, either hiccupping or giggling, swallowed convulsively...#:-0))

As for increasing your chances: if you take 1-2 tickets, then count the increase as zero. If you start to really increase, the game will be at a loss, because there is no guarantee that in the end everything will pay off.

The daily audience of the Proza.ru portal is about 100 thousand visitors, who in total view more than half a million pages according to the traffic counter, which is located to the right of this text. Each column contains two numbers: the number of views and the number of visitors.

Today we will talk about how to calculate or guess 100 percent winning lottery number. We will also consider methods and technologies for calculating winning number combinations in lotteries, allowing you to be guaranteed to win

Training video on how to win the lottery:

YouTube Video

It must be admitted that intuitive gaming systems have helped some lucky players win the lottery more than once. But most of those who prefer to play according to the system still choose strict calculation. Before going for lottery tickets, they study in detail the history of the draws, analyze the combinations that came out, and build mathematical systems for playing the lottery.

Pythagoras and other great minds of antiquity tried to calculate the probability of winning the lottery. Alan Kriegman devoted many scientific works to this topic, trying to calculate the chances of an individual player winning the Keno lottery. In his opinion, this chance directly depends on the number of bets made by the player; in other words, the more lottery tickets he fills, the higher the probability of winning.

This theory was confirmed in practice by another mathematician, Stefan Mendel, in 1992. He helped a syndicate of 2.5 thousand people hit the jackpot in the Virginia State Lottery. According to the scientist’s calculations, in the lottery, which was drawn according to the “6 out of 44” scheme, only 7,059,052 non-repeating number combinations were obtained. If you mark them all on the tickets, you will definitely win. True, you will have to spend money on tickets - $1 each, total: a little more than $7 million.

The syndicate participants simply waited until the game's jackpot significantly exceeded the planned expenses, then they began to play the lottery. Several thousand players began to buy lottery tickets in an organized manner at points of sale and in online stores. It took 72 hours, but the game was worth the candle! Fans of mathematical calculations managed to win more than 27 million dollars in the lottery, about 10 thousand for each player.

Another popular mathematical system for playing the lottery is frequency analysis. This method is based on the fact that in each game there are “hot” (dropped most often) and “cold” (dropped least often) numbers. They are calculated by analyzing the results of previous games. Afterwards, the player, depending on his own preferences, bets either on “hot” or “cold”, or combines. There are cases in the history of lotteries when such a system helped to win the lottery big. For example, Janey Callus from Texas used frequency analysis to play a local lottery and won a $21.8 million jackpot.

Another option for using mathematics to play the lottery: complete (“drum”) and incomplete systems. The reel system of the game comes down to using all possible combinations of a limited range of numbers. For example, if you need to guess 6 numbers, take at least 7 of any numbers found in the lottery and make 7 combinations from them. It turns out the following:

1. 1, 2, 3, 4, 5, 6

2. 1, 2, 3, 4, 5, 7

3. 1, 2, 3, 4, 6, 7

4. 1, 2, 3, 5, 6, 7

5. 1, 2, 4, 5, 6, 7

6. 1, 3, 4, 5, 6, 7

7. 2, 3, 4, 5, 6, 7

The numbers in the combinations are repeated, as if “spinning in a drum,” which is why the game system received the corresponding name. It is called complete because all existing combinations of selected numbers are used. You can guess that playing the lottery using such a system is quite expensive, since you need to purchase a lot of tickets. To cut costs, players created an incomplete system.
. The incomplete lottery system cuts off some combination options at the player's discretion. For example, if you need to guess the same 6 numbers, according to the incomplete system, only 5 combinations of 7 numbers are made:

1. 1, 2, 3, 4, 6, 7

2. 1, 2, 3, 5, 6, 7

3. 1, 2, 4, 5, 6, 7

4. 1, 3, 4, 5, 6, 7

5. 2, 3, 4, 5, 6, 7

Fans of these game schemes add that the systems still do not guarantee a 100% win, but third- and fourth-order prizes help you win often.
Pros and cons of mathematics in lotteries

Mathematical systems for playing the lottery have both supporters and opponents. Their use is supported by some examples of large winnings in the history of lotteries and the fact that playing according to the system increases the player’s involvement in the process, forcing him to regularly place bets, and this often leads to winnings.
A number of scientists are against mathematical systems for playing the lottery. They generally argue that predicting a lottery is not a rewarding task and it is impossible to calculate the probability of winning the lottery. Thus, Doctor of Physical and Mathematical Sciences, Professor Petr Zaderey is sure: the numbers of balls that fall out on the lottery machine are random variables that cannot be analyzed mathematically. Another mathematician, Pavel Lurie, claims that the probability of winning the lottery is determined randomly and the chances of each player are absolutely equal.

However, we should not forget that even scientists sometimes make mistakes, and many great discoveries were not taken seriously at first. Perhaps you will be the one to invent your own system for calculating the probability of winning the lottery. The main thing is to play and not give up if you don’t hit the jackpot the first time. And how to play the lottery, using mathematical systems or one’s own intuition, is up to everyone to decide for themselves.

It turns out that success and luck have a simple mathematical formula. It was developed by Richard Weissman, a professor at the University of Hertfordshire (UK). Moreover, he not only compiled an abstract formula for success, but was also able to back it up with practical evidence.

"The Luck Factor"

This is the name of the scientific work published by Weissman. For many years he searched for the answer to the eternal question: why do some people manage to attract good luck, while others remain losers all their lives? The professor conducted a colossal study, the results of which were supported by a number of experiments.

At the initial stage of the project (in 1994), the scientist advertised in the local newspaper, in which he invited volunteers aged 18 to 84 years old, who considered themselves lucky and unlucky, to cooperate. In total there were about 400 people, approximately equally divided between both. For 10 years, they must undergo interviews, keep diaries, fill out various questionnaires, answer IQ tests, and participate in experiments.

For example, once the subjects were given the same issue of a newspaper in which they had to count all the photographs. Those who consider themselves lucky completed the task in a couple of minutes, while the unlucky ones needed much more time. The secret of the experiment was that already on the second page of the publication there was a large announcement: “This newspaper contains 43 photographs.” Since it itself was not accompanied by a photo, the losers did not even pay attention to it and painstakingly continued to complete the task assigned to them. And the “lucky ones” immediately found the clue.

“Lucky people look at the world with their eyes wide open, they don’t miss happy accidents. And the unlucky ones are usually immersed in their worries and do not notice anything “extra,” Professor Weissman explained in his scientific article.

In addition, lucky people are sociable; they are not afraid of changing places and making new acquaintances, which often turn out to be useful to them later. People who consider themselves unlucky, on the contrary, try to close themselves off from the outside world and live within the existing framework.

For this, the scientist has developed a special self-development technique that helps attract good luck. Four simple rules must be followed:

· Pay attention to everything that happens around you, learn to notice the signs of fate and take advantage of a happy occasion.

· Develop intuition, trust the “inner voice”.

· Think about the good: drive away bad thoughts and tune in to the positive.

· Learn to enjoy life in any, even the most difficult, situations.

The ability to look for positive moments even in unpleasant situations is the key to success. Psychologists have long discovered that some people, in difficult times, are able not to concentrate on troubles, but to think that things could have been worse. This feature of the psyche helps to “soften the blow” and feel lucky. This was confirmed by Professor Weissman’s “lucky” and “unlucky” people. They would have assessed the situation differently if they had been held hostage during a bank robbery and had been shot in the arm. The first considered it to be luck, since they could have died altogether. The second decided that this was a big failure, since there might not have been any injury at all.

British studies have proven that “luck”, “fortune”, “success” are subjective concepts. Any individual himself determines who he is: lucky or unlucky. Science has confirmed that a lot depends on a person’s mood and his perception of the surrounding reality.

A striking example is 54-year-old John Lin from the UK. He is called the most unlucky resident of the country. During his life, he managed to get into 20 accidents. When he was very young, John was seriously injured when he fell out of his carriage, then fell off his horse and was hit by a car. As a teenager, he suffered fractures from falling from a tree. And when he was returning from the hospital, where he was treated after this fall, his bus got into an accident and the guy again ended up in a hospital bed. As an adult, Lin was involved in accidents three more times. In addition, he is constantly haunted by natural disasters: for example, a rockfall or lightning, which struck him twice, although the chance of even one lightning strike on a person, according to the US National Weather Service, is only 1 in 600,000.

However, one can approach this list of troubles in different ways. After all, in each of the accidents, any other person could have simply died, but John Lin always survived. So maybe this is not bad luck, but, on the contrary, luck? “I can’t explain why all this is happening to me,” John shared with reporters. “But every time I’m glad I’m alive.”

This is exactly how Richard Weissman advises to perceive any failures. The main thing is to be positive. Thus, if, having decided to try his luck and buy lottery tickets, a person thinks that he will never be lucky, then luck will not smile on him. And if you believe in victory and continue to play the lottery regularly, even after several unsuccessful draws, you will definitely win a million!

The so-called intuitive strategies, that is, playing according to a system based on one’s own “sixth sense,” are very popular among experienced players. For example, a person is sure that his lucky number is 3. In this case, when filling out lottery tickets, you should mark all the derivatives of this number: 3, 9, 18, 24, etc. Or numbers in which three appears: 13, 23, 33, 53 and so on. We wrote about how to find your lucky number in previous materials.

Another way to increase your probability of winning is to select numbers using a specific step. For example, in a combination of 7, 14, 21, 28, 35, the step will be 7. The step can again be the player’s lucky number or any other number.

Intuitive strategies include the so-called “zigzag of luck.” If you play according to this system, then you need to mark the numbers in such a way that they form a zigzag or other “lucky figure”. Some, for example, cross out all the numbers vertically, some cross them, and others generally in the form of certain letters of the alphabet.

Perhaps the main advantage of playing the system is its consistency. That is, the player systematically works out various combinations, looking for the key to his luck. If you play the system regularly, the probability of winning will most likely increase significantly.

The pendulum of luck, or how to win a million in the lottery Anyone can win a million; all you need for this is luck, luck and a lucky lottery ticket. However, some experienced players do not want to wait long for luck to knock on their door, preferring to lure it in as quickly as possible.

For this, everyone has their own secrets of success. One of them is the use of a pendulum of luck.

The principle of the pendulum has excited the minds of people since ancient times; it was credited with mystical powers, the ability to predict the future and find answers to the most difficult questions. Just remember the popular sessions of collective magic, when with the help of a homemade pendulum, girls told fortunes about their betrothed or asked for help in making important decisions.
It turns out that the pendulum can also be useful to lottery lovers in their hunt for winnings. Using a pendulum is one of the types of dowsing. One of its first manifestations in the history of mankind was the so-called dowsing, when a priest or prophet, with the help of a vine, found a source of water hidden underground.

Similarly, when playing the lottery, the pendulum helps a person find an equally important source of wealth, that is. Scientists still have not agreed on what dowsing is. Some say that the vine or pendulum is made to move by the person himself, or rather by his involuntary movements and vibrations controlled by the subconscious (ideomotor reaction).

In any case, for some this practice helps to find hidden objects, for others. Using a pendulum to play the lottery is very simple.

To do this, you will need a strong thread or a thin chain about 40 centimeters long (a person chooses the length that is convenient for him in the process) and a small weight, the weight of which does not exceed 40 grams. Fans of this method advise using a wedding ring (without any inserts) or a pendant made of natural stone (for example, amber or amethyst). It is important that the shape of the load is symmetrical.

Let us make a reservation that the pendulum can only be used to predict winnings. To do this, you need to hang the load on a thread, take the resulting pendulum in your right hand and hold it suspended.

Place a lottery ticket or a plate with the numbers used in the selected lottery on the table (for example, if in a lottery you need to guess 5 numbers out of 36, then the table should have 36 numbers). The numbers should be written quite large so that the player can hold the pendulum over each of them and determine the nature of its movements. So, the table (or lottery ticket) is placed on the table, you need to place a pendulum over each number and wait until it starts to swing.

It is generally accepted that if the weight begins to swing clockwise, this means a positive answer, that is, there is a high probability that a ball with this number will appear in the next lottery draw. If the pendulum moves counterclockwise over a number, then the probability of it falling out is very low.

Thus, you need to hold the pendulum over each number and select those over which it rotated clockwise. If he points to more numbers than you need to guess in the lottery, you can make an expanded bet or mark all the numbers selected by the pendulum in them. Then wait until the lottery draw takes place and check if you are lucky enough to win a million.

It is important to remember that in order to use a pendulum to select lucky numbers to fill out a lottery ticket, you must choose a secluded place where no one can interfere with the upcoming magical session. You also need to be extremely focused on the desire to win the lottery, believe in victory and not give up if you didn’t hit the jackpot the first time.

And the surest way to increase the likelihood of winning the lottery is to buy as many as possible, one of them will definitely be a winner!

An important branch of mathematics, which is also used in other exact sciences, is called combinatorics. Most people do not even have a basic understanding of this science. Although they are very easy to understand. To do this, it is enough to have arithmetic counting skills and be familiar with the basic four mathematical operations.
Most likely, the use of combinatorics in everyday life will not be necessary, although in some areas of activity it can be very useful.

The method of arranging a number of different objects in the form of a sequence is called permutation. It looks like this - this will be the first, this will be the third, etc.
The role of an object can be played by absolutely any objects - signs, figures, numbers, things, etc. The easiest way to explain the principle of permutation is using simple integers.
A set of numbers from 5 to 8 can be represented as the following permutations - 5678 or 5876, etc. It turns out that any four digits can be arranged in 24 ways. Therefore, the more numbers there are in a set, the wider the number of ways to arrange them.
Two numbers have only two ways of arrangement: 36 and 63.
Three numbers have six ways of arrangement.

To determine the number of options, place 5 numbers, you need to try and in the end you will get 120 options.
However, there is a simpler option for determining the number of different arrangements of numbers in any number set.
You just need to multiply all the numbers from 1 to the number of objects in the set of numbers.
This rule can be easily confirmed with the following example. A set of one number has one set of ways. A set of two numbers has two sets (2*1=2). A set of three numbers has 6 possible sets and so on -
This mathematical operation is called factorial, and its symbol is an exclamation point! Pronounced "factorial of three" or "three factorial".
Thus we obtain the desired formula, which follows from the formulation of the imperial and determines its main property.

For example, a certain number of balls – n – take part in a lottery draw. After the lottery, only k numbers will appear in the draw, which will become lucky. Therefore, the number of options for dropping balls is the number of combinations of these two quantities. By substituting the numbers of different runs and the number of balls involved in them into the formula (n, k), we get the exact number of combinations.

Using these simple calculations, you can get numbers that accurately indicate the chance of winning the jackpot when purchasing one ticket. For "SuperLoto" 1 chance in 13,983,816 = 0.0000000715, and for "MEGALOT" 1 chance in 52,457,860 = 0.0000000191. Values ​​of C(k, n) for k = 1:20. Whether this is a lot or a little, judge for yourself, but keep in mind that this is when purchasing a single ticket.

You can also consider the reality of guessing a single partial combination. What is the probability of guessing M numbers, taking into account filling in N fields. The circulation contains C(20, M). therefore, the probability of getting the desired combination is C(20, M) / C(80, M). If N cells are filled in the set, then there will be C(N, M) options consisting of M digits. Therefore, the possibility that one of the balls will fall out is equal to the calculation amount, C(N, M) C(20, M) / C(80, M). For example:9 out of 10

(N, M) С(T, M) / С(B, M)
B – number of balls with numbers used in the lottery
T – the number of balls that are drawn during the draw
N – number of cells filled by the player
M is the number of lucky balls for which the calculation is performed.

It should be remembered that the formula C(N, M) C(T, M) / C(B, M) is not perfectly accurate, it is approximate, but when calculated using small numbers, the error is negligible and does not influence the result.

Many people use various techniques and programs in the hope of winning a large sum in the lottery. But almost every one of these methods is based on faulty logic. After all, if significant programs for selecting a winning combination were freely available, then the lottery would completely lose its concept: all numbers are equally probable.

What is the paradox of lotteries?

Developers of both Russian and foreign programs for selecting lottery combinations claim:
— programs are not a simple random number generator, but a powerful mathematical and analytical tool for those who play and want to win, based on statistical analysis;
— programs allow you to control the lottery game, and not guess, selecting the next combination;
— the software saves money by applying filters that eliminate unlikely combinations;
— programs analyze various types of probabilities based on previous draws.

Some of these programs are offered to lottery fans to purchase for a small amount. Paid systems have advanced functionality. For example, a customizable number generator, in which you can include a sum filter and “a mode for overlaying played combinations on top of each other to obtain alternative statistics.”

In addition, Gayle Howard’s book “Lottery Master Guide,” priced at $24.50, is very popular online. According to the author, this is the most complete and complete guide to lottery strategies and selection of number combinations. “You'll learn how to identify specific numbers for specific lotteries and won't waste any more money. After reading the guide, you will know the world's best methods to win lotteries. You will improve your luck with the help of knowledge and skills,” reads the summary of the book. In addition, it is claimed that 107 people have already become winners of various lotteries thanks to the management (the count of winnings has been kept since 1985).

Gayle is advised to choose even and odd numbers for her combinations. In addition, it is stated that if you play with six numbers, then their sum must be in the range from 106 to 170.

Unfortunately, no number matching program can guarantee an accurate hit. If developers claim otherwise and distribute software for a fee, then this is fraud. So far, not a single millionaire of the Russian state lottery has said that he used some kind of program to select numbers, especially one purchased on the Internet. You can increase your chances of winning, but in completely different ways. Statistics of Russian state lotteries, archives of draws with winning combinations - everything you need to win is provided for each participant on the Stoloto website absolutely free of charge.

Remember, the paradox of lotteries is that the probability of winning a particular ticket is small, but the probability of winning any ticket is one, that is, 100%. This means only one thing: combinations 1, 3, 6, 10, 12 and 15, 20, 22, 31, 36 are equally probable and can occur in any of the draws.

Statistics on the Stoloto website

Of course, you can use number matching programs for fun or as a new method of playing. But we still strongly discourage you from purchasing paid software. With this amount you can make, for example, several more bets, which will increase your chances in proportion to the number of tickets purchased. And you will find all statistical data on the website. To avoid becoming a victim of another scammer, read this.

In the “Draw Archive” for each Russian lottery there are statistics on numbers drawn both for the entire time and for the last 10 draws:

An example of statistical data for the Gosloto 5 out of 36 lottery

Russian Lotto lottery statistics

Also, after registering on the site, each participant has the opportunity to estimate the number of occurrences of each number (the picture shows a graph of the occurrence of all numbers in the Gosloto “6 out of 45” lottery).

Frequently dropped pairs of numbers in the Gosloto “5 out of 36” lottery. Any number can be added to your bet.

In lotteries using the bingo system (Russian Lotto and Housing Lottery), a participant can select tickets either manually or by selecting “All numbers” from 1 to 90. In addition, in all lotteries you can use the “Favorite numbers” option.

And here is the combination that brought Igor S. more than 47 million rubles in Gosloto “5 out of 36”. Who could predict the probability that 2 pairs of numbers will follow each other? The answer was given by Igor himself: “I have my own way, which I follow. But I won’t reveal its secret.. When I think about what numbers to mark, I follow it from time to time. I look at frequently dropped numbers, for example. Why do I never bet big? I don't see much point in this. I believe that you can win with a small bet. You will either be lucky or not.”

Even if you take the time to study our statistics inside and out, you still will not have an absolute guarantee of winning. Winning the lottery is always a matter of chance, and no one can know the winning combination in advance. This is confirmed by our millionaires. Peter T. won more than 8 million rubles in the 2512th draw of Gosloto “5 out of 36”. The combination of 19, 5, 9, 35, 23 brought him success: “Over the years of participating in lotteries, I have tried many different schemes and formulas. I followed signs, kept track of lucky days, tried to find my lucky numbers, but it’s impossible to outwit luck. In the end, I won with completely random numbers.”

Andrey P., who won more than 6 million rubles in Gosloto 5 out of 36, says: “I choose the numbers according to how my hand falls and where my eye looks. I’m a cheerful person, and I’m not interested in calculating anything, I’d rather talk to my friends at this time.”

Two sisters from Murmansk, Tatyana and Lyudmila T., won a huge amount in Gosloto “6 out of 45” - more than 100 million rubles. And the secret of their victory is simple: “We buy lottery tickets on the eve of the birthday of one of our relatives. It was grandpa's birthday."

Natalya Kireeva won a million rubles in the Russian Lotto and explained her luck this way: “Everything happened spontaneously. A long time ago I saw a program on TV about lottery winners. And for some reason I remembered her when I walked past the lottery kiosk. She came up to him, then left again, as if something was pulling her. I took this attraction as a sign and bought a ticket. Then on Sunday I woke up two minutes before the start of the Russian Lotto program. Also a sign! Right up until the drawing itself, I was sure that I would win, even if it was a small amount. But, of course, I didn’t expect a million rubles!”

These examples are proof that in lotteries everything is decided by chance. And each of you has a chance to hit the jackpot. Therefore, you should not waste your time searching for programs on the Internet that provide “magic guarantees” or “predict combinations.” Under no circumstances should you be deceived if you are offered to tell you what numbers will appear in tomorrow’s draws, even for a small sum. We tell you with a 100% guarantee that only scammers do this. To be fully armed, read ours, and be vigilant!

Mobile application "Stoloto"

Your whole life is on the run and you don’t have time to go to a lottery kiosk? With ours, all problems will disappear overnight. After downloading it, you can purchase a ticket at any time, find out the results of previous draws, top up your Stoloto wallet and read about the latest news in the world of lotteries. The Stoloto application is available in two versions: for Android and iOS. Choose the version that suits your smartphone and use the most convenient and fastest way to buy lottery tickets.